前言
前面介绍学习的大多是线性表相关的内容,把指针搞懂后其实也没有什么难度,规则相对是简单的,后面会讲解一些比较常见的数据结构,用多图的方式让大家更容易吸收。
在数据结构与算法中,树是一个比较大的家族,家族中有很多厉害的成员,这些成员有二叉树和多叉树(例如B+树等),而二叉树的大家族中,二叉搜索树(又称二叉排序树)是最最基础的,在这基础上才能继续拓展学习AVL(二叉平衡树)、红黑树等知识。
对于二叉排序树而言,本章重点关注其实现方式以及插入、删除步骤流程,我们会手写一个二叉排序树,二叉树遍历部分的内容比较多会单独详细讲解。
什么是树
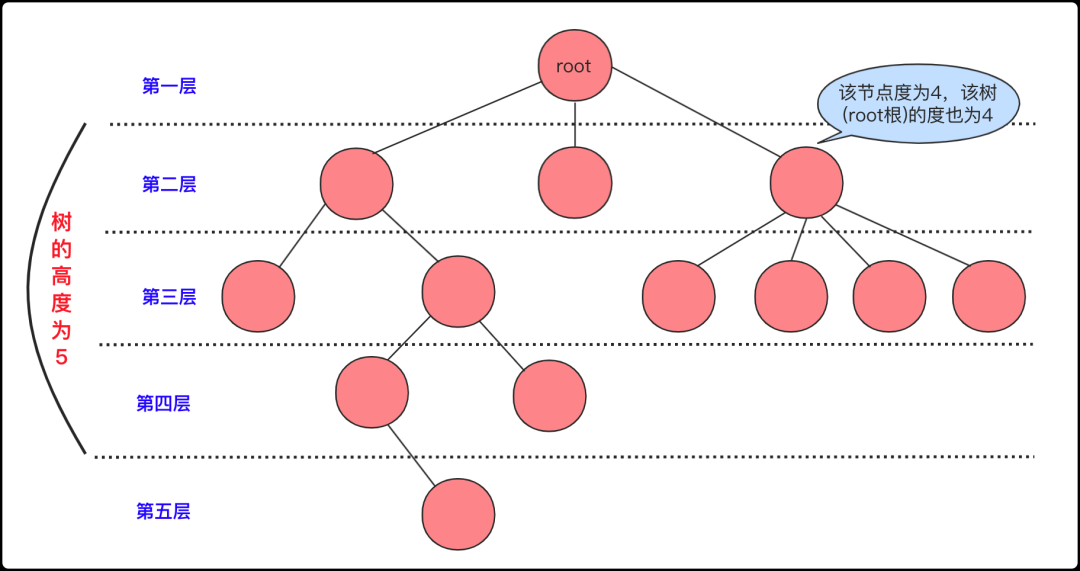
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树是递归的,将树的任何一个节点以及节点下的节点都能组合成一个新的树,所以树的很多问题都是使用递归去完成。
根节点: 最上面的那个节点(root),根节点没有父节点,只有子节点(0个或多个都可以)
层数: 一般认为根节点是第1层(有的也说第0层),而树的高度就是层数最高(上图层数开始为1)节点的层数
节点关系:
- 父节点:连接该节点的上一层节点,
- 孩子节点: 和父节点对应,上下关系。而祖先节点是父节点的父节点(或者祖先)节点。
- 兄弟节点:拥有同一个父节点的节点们!
节点的度: 就是节点拥有孩子节点的个数(是直接连接的孩子不是子孙).
树的度: 就是所有节点中最大 (节点的度)。同时,如果度大于0的节点是分支节点,度等于0的节点是叶子节点(没有子孙)。
相关性质:
二叉树
二叉树是一树的一种,但应用比较多,所以需要深入学习,二叉树的每个节点最多只有两个子节点(但不一定非得要有两个节点)。
二叉树与度为2的树的区别:
1、度为2的的树必须有三个节点以上(否则就不叫度为二了,一定要先存在),二叉树可以为空。
2、二叉树的度不一定为2,比如斜树。
3、二叉树有左右节点区分,而度为2的树没有左右节点的区分。
几种特殊二叉树:
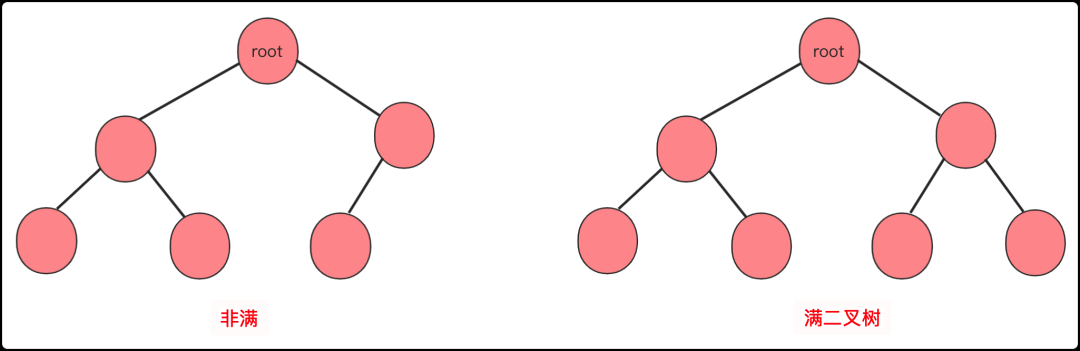
满二叉树:高度为n的满二叉树有(2^n) -1个节点
满二叉树
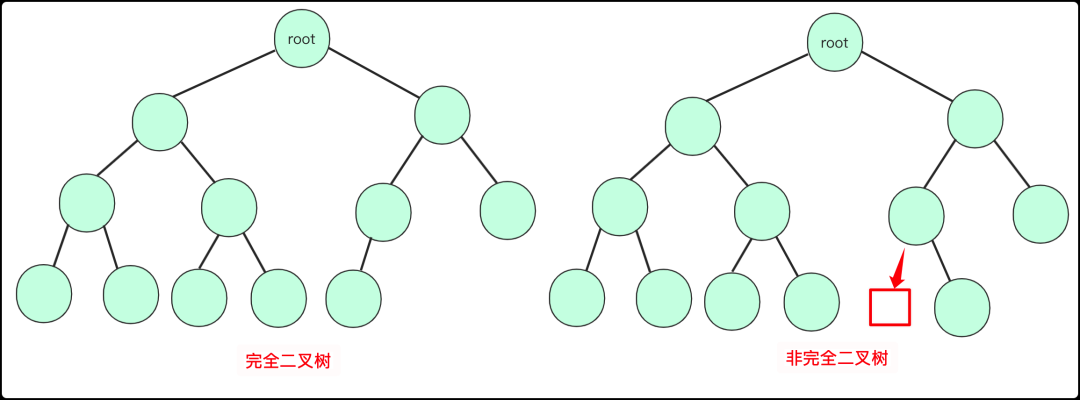
完全二叉树:上面一层全部满,最下一层从左到右顺序排列
完全二叉树
二叉排序树:树按照一定规则插入排序(本文详解)。
平衡二叉树:树上任意节点左子树和右子树深度差距不超过1(后文详解).
二叉树性质:
1、二叉树有用树的性质
2、非空二叉树叶子节点数=度为2的节点数+1.本来一个节点如果度为1.那么一直延续就一个叶子,但如果出现一个度为2除了延续原来的一个节点,会多出一个节点需要维系。所以到最后会多出一个叶子。
3、非空第i层最多有2^(i-1)个节点。
4、高为h的树最多有(2^h)-1个节点(等比求和)。
二叉树一般用链式存储,这样内存利用更高,但二叉树也可以用数组存储的(经常会遇到),各个节点对应的下标是可以计算出来的,就拿一个完全二叉树若从左往右,从上到下编号如图:
二叉树节点位置对应关系
二叉排序(搜索)树
概念
前面铺垫那么多,咱们言归正传,详细讲解并实现一个二叉排序树,二叉搜索树拥有二叉树的性质,同时有一些自己的规则:
首先要了解二叉排序树的规则:从任意节点开始,节点左侧节点值总比节点右侧值要小。
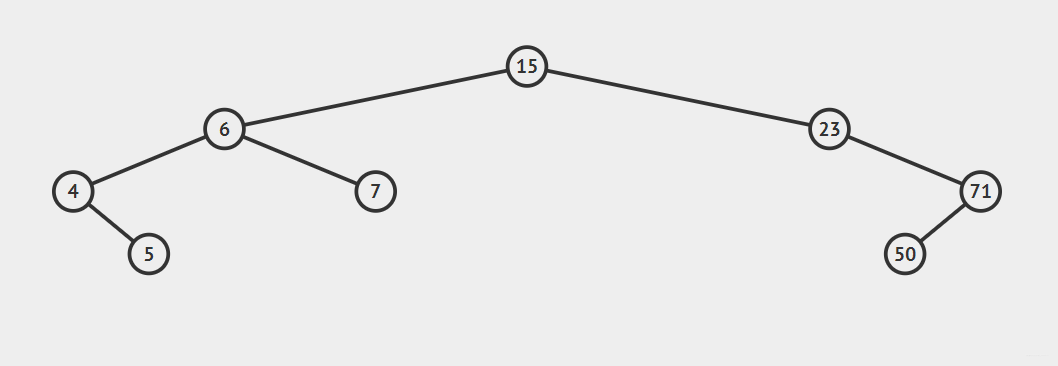
例如一个二叉排序树依次插入15,6,23,7,4,71,5,50会形成下图顺序
一个二叉排序树
构造
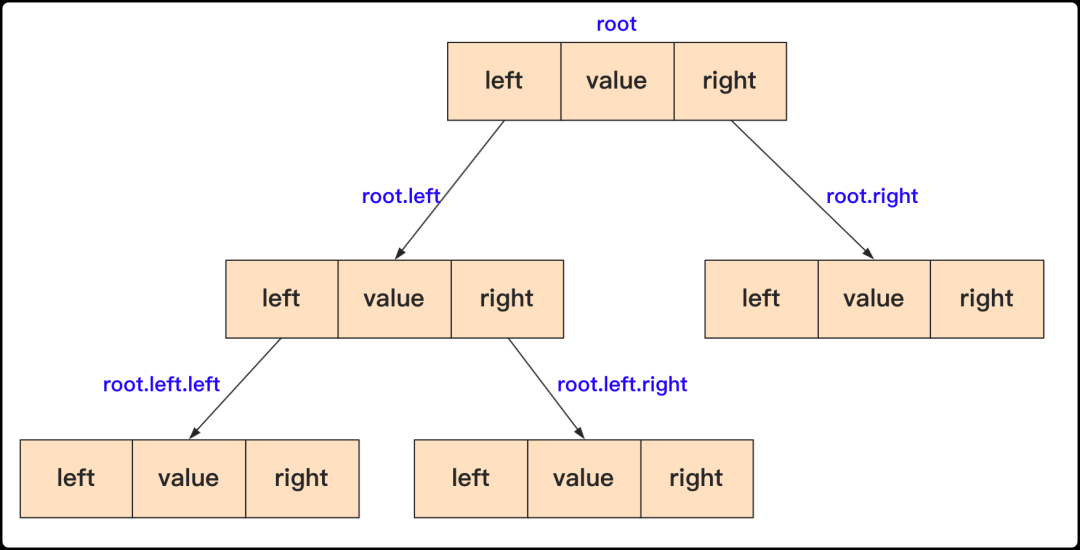
二叉排序树是由若干节点(node)构成的,对于node需要这些属性:left,right,和value。其中left和right是左右指针指向左右孩子子树,而value是储存的数据,这里用int 类型。
node类构造为:
- classnode{//结点
- publicintvalue;
- publicnodeleft;
- publicnoderight;
- publicnode()
- {
- }
- publicnode(intvalue)
- {
- this.value=value;
- this.left=null;
- this.right=null;
- }
- publicnode(intvalue,nodel,noder)
- {
- this.value=value;
- this.left=l;
- this.right=r;
- }
- }
既然节点构造好了,那么就需要节点等其他信息构造成树,有了链表构造经验,很容易得知一棵树最主要的还是root根节点。
所以树的构造为:
- publicclassBinarySortTree{
- noderoot;//根
- publicBinarySortTree()
- {root=null;}
- publicvoidmakeEmpty()//变空
- {root=null;}
- publicbooleanisEmpty()//查看是否为空
- {returnroot==null;}
- //各种方法
- }
可以用图来表示一下这个结构:
主要方法
既然已经构造好一棵树,那么就需要实现主要的方法,因为二叉排序树中每个节点都能看作一棵树。所以我们创建方法的是时候加上节点参数(方便一些递归调用)
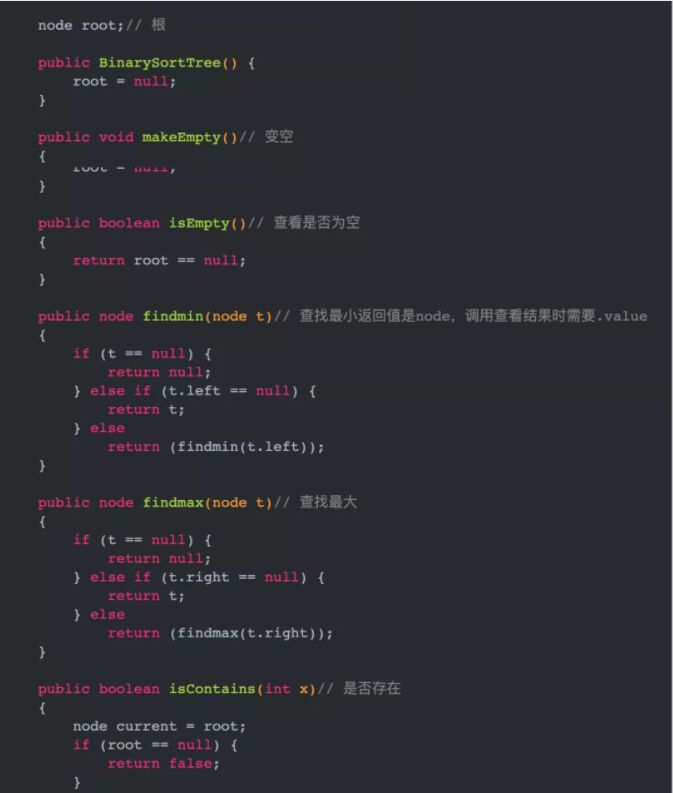
findmax(),findmin()
findmin()找到最小节点:
因为所有节点的最小都是往左插入,所以只需要找到最左侧的返回即可,具体实现可使用递归也可非递归while循环。
findmax()找到最大节点:
因为所有节点大的都是往右面插入,所以只需要找到最右侧的返回即可,实现方法与findmin()方法一致。
代码使用递归函数
- publicnodefindmin(nodet)//查找最小返回值是node,调用查看结果时需要.value
- {
- if(t==null){returnnull;}
- elseif(t.left==null){returnt;}
- elsereturn(findmin(t.left));
- }
- publicnodefindmax(nodet)//查找最大
- {
- if(t==null){returnnull;}
- elseif(t.right==null){returnt;}
- elsereturn(findmax(t.right));
- }
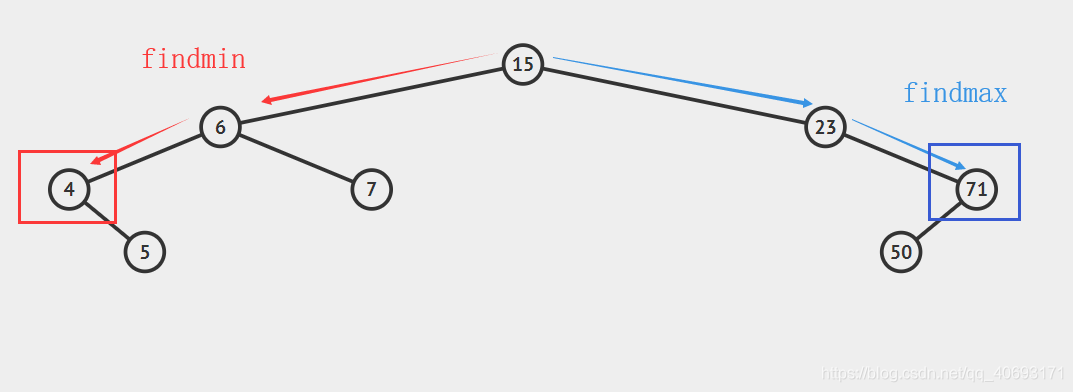
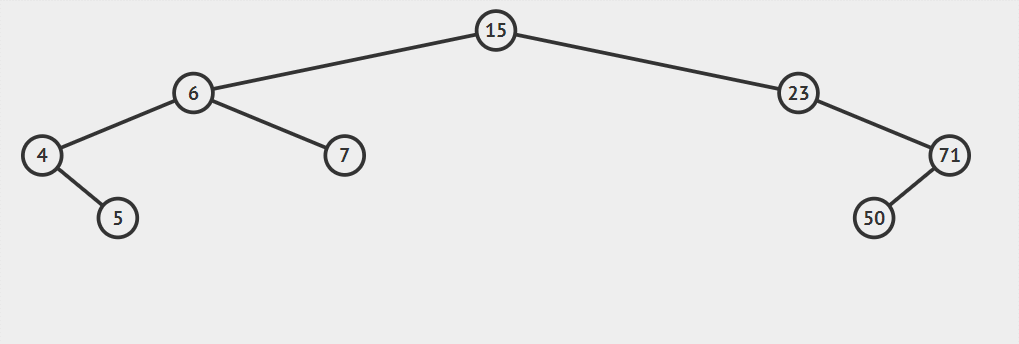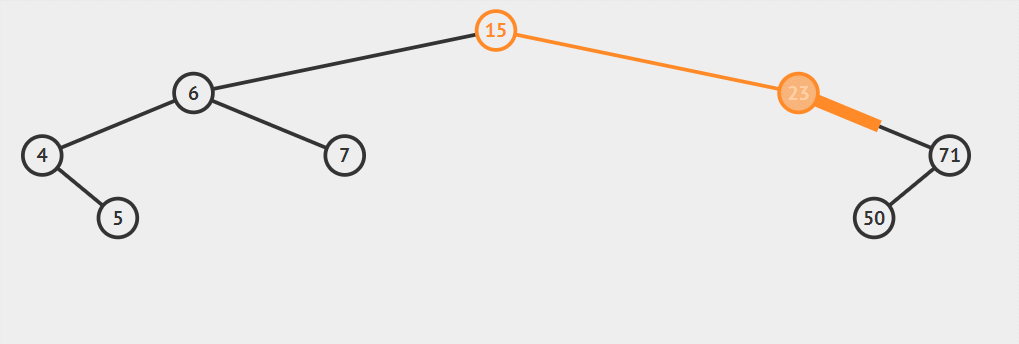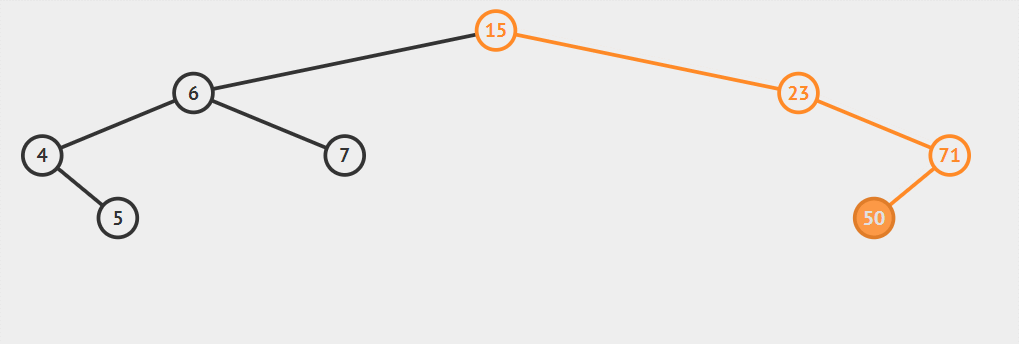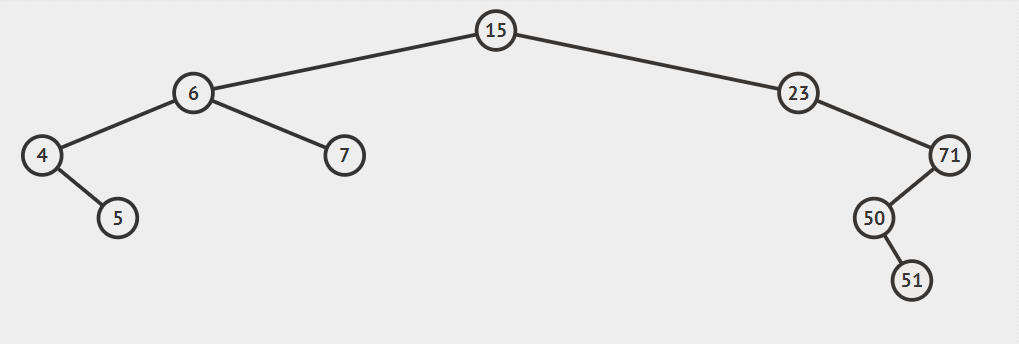
一个图中查找最大最小过程如下:
查找过程
isContains(int x)
这里的意思是查找二叉查找树中是否存在值为x的节点。
在具体实现上,根据二叉排序树左侧更小,右侧更大的性质进行往下查找,如果找到值为x的节点则返回true,如果找不到就返回false,当然实现上可以采用递归或者非递归,我这里使用非递归的方式。
- publicbooleanisContains(intx)//是否存在
- {
- nodecurrent=root;
- if(root==null){returnfalse;}
- while(current.value!=x&¤t!=null)
- {
- if(x<current.value){current=current.left;}
- if(x>current.value){current=current.right;}
- if(current==null){returnfalse;}//在里面判断如果超直接返回
- }
- //如果在这个位置判断是否为空会导致current.value不存在报错
- if(current.value==x){returntrue;}
- returnfalse;
- }
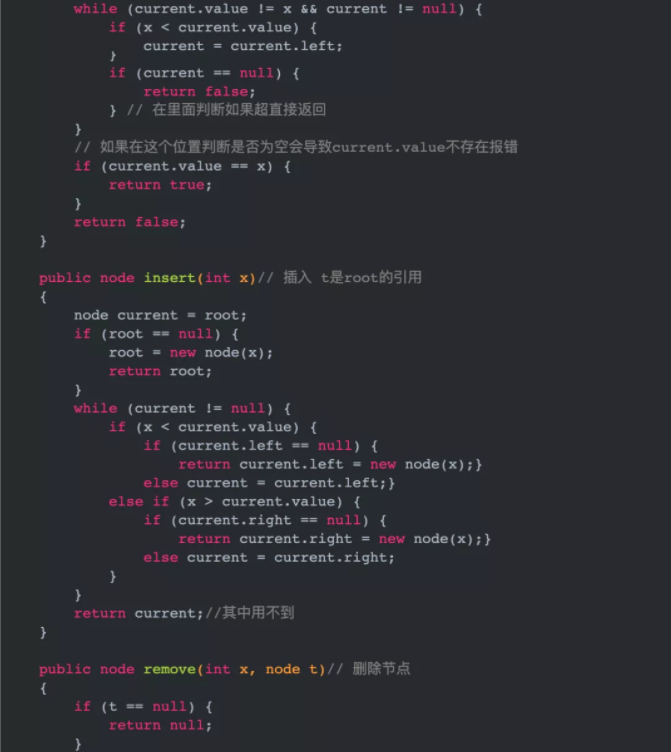
insert(int x)
插入的思想和前面isContains(int x)类似,找到自己的位置(空位置)插入。
但是具体实现上有需要注意的地方,我们要到待插入位置上一层节点,你可能会疑问为什么不直接找到最后一个空,然后将current赋值过去current=new node(x),这样的化current就相当于指向一个new node(x)节点,和原来树就脱离关系(原树相当于没有任何操作),所以要提前通过父节点判定是否为空找到位置,找到合适位置通过父节点的left或者right节点指向新创建的节点才能完成插入的操作。
- publicnodeinsert(intx)//插入t是root的引用
- {
- nodecurrent=root;
- if(root==null){
- root=newnode(x);
- returnroot;
- }
- while(current!=null){
- if(x<current.value){
- if(current.left==null){
- returncurrent.left=newnode(x);}
- elsecurrent=current.left;}
- elseif(x>current.value){
- if(current.right==null){
- returncurrent.right=newnode(x);}
- elsecurrent=current.right;
- }
- }
- returncurrent;//其中用不到
- }
比如说上面树插入值为51的节点。
插入值为51的节点
delete(int x)
删除操作算是一个相对较难理解的操作了,因为待删除的点可能在不同位置所以具体处理的方式也不同,如果是叶子即可可直接删除,有一个孩子节点用子节点替换即可,有两个子节点的就要先找到值距离待删除节点最近的点(左子树最大点或者右子树最小点),将值替换掉然后递归操作在子树中删除已经替换的节点,当然没具体分析可以看下面:
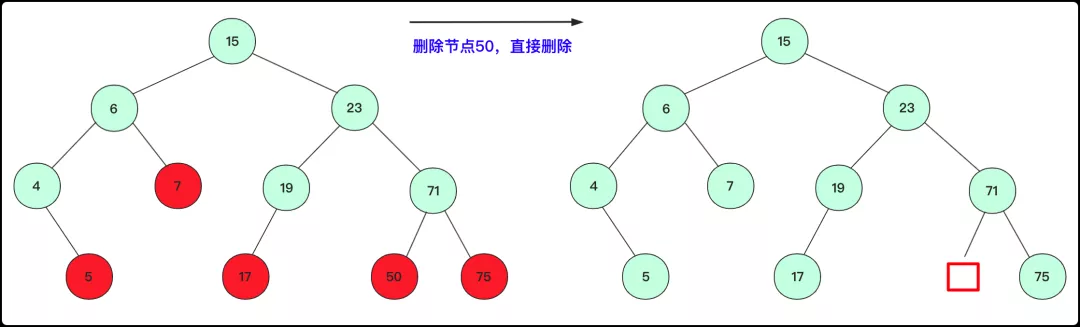
删除的节点没有子孙:
这种情况不需要考虑,直接删除即可(节点=null即可)(图中红色点均满足这种方式)。
待删除节点为叶子节点
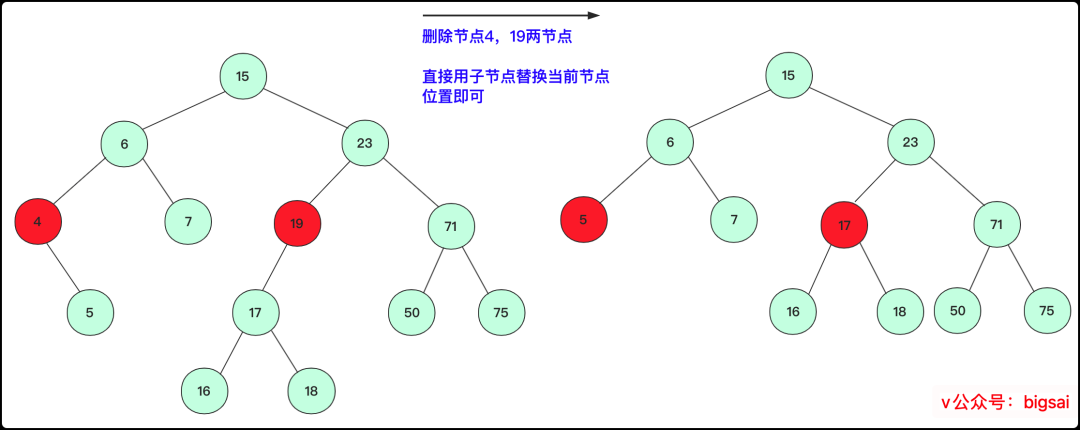
一个子节点为空:
此种情况也很容易,直接将删除点的子节点放到被删除位置即可。
待删除节点有1个孩子
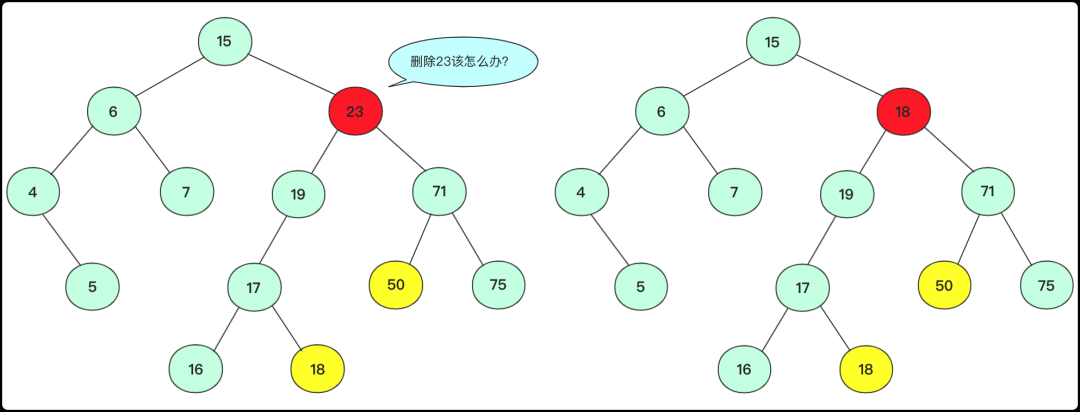
左右节点均不空
左右孩子节点都不为空这种情况是相对比较复杂的,因为不能直接用其中一个孩子节点替代当前节点(放不下,如果孩子节点也有两个孩子那么有一个节点无法放,例如拿下面71节点替代)
待删除节点有两个孩子
如果拿19或者71节点填补。虽然可以保证部分侧大于小于该节点,但是会引起合并的混乱.比如你若用71替代23节点。那么你需要考虑三个节点(19,50,75)之间如何处理,还要考虑他们是否满,是否有子女,这是个复杂的过程,不适合考虑。
所以,我们要分析我们要的这个点的属性:能够保证该点在这个位置仍满足二叉搜索树的性质(找到值最近的),那么子树中哪个节点满足这样的关系呢?
左子树中最右侧节点或者右子树中最左侧节点都满足,我们可以选一个节点将待删除节点值替换掉(这里替换成左子树最右侧节点)。
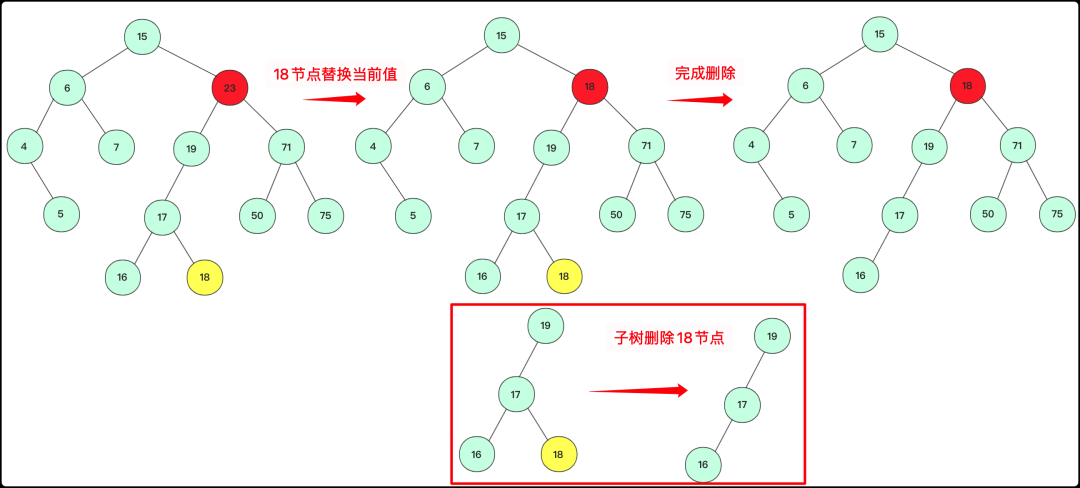
这个点替换之后该怎么办呢?很简单啊,二叉树用递归思路解决问题,再次调用删除函数在左子树中删除替换的节点即可。
先替换值再递归在子树中删除18节点
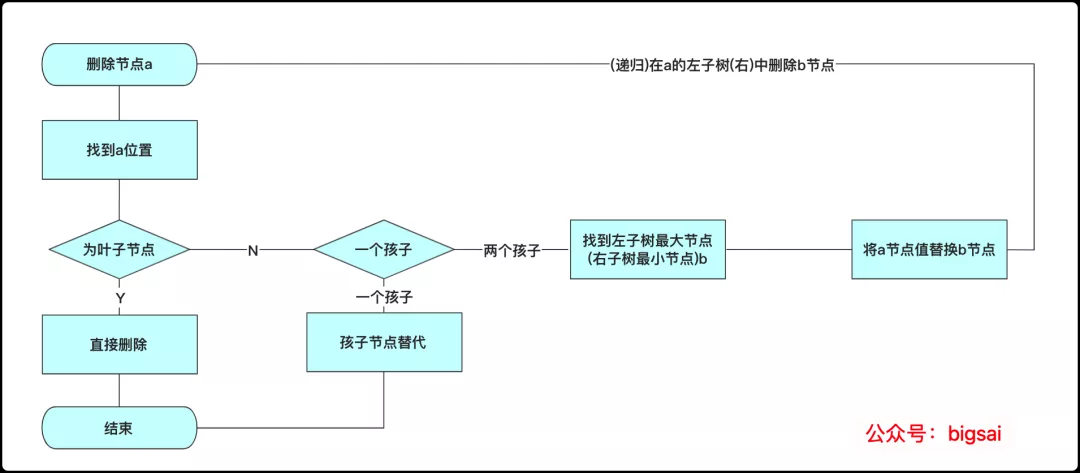
这里演示是选取左子树最大节点(最右侧)替代,当然使用右子树最小节点也能满足在这待删除的大小关系,原理一致。整个删除算法流程为:
删除流程
这部分操作的代码为:
- publicnoderemove(intx,nodet)//删除节点
- {
- if(t==null){
- returnnull;
- }
- if(x<t.value){
- t.left=remove(x,t.left);
- }elseif(x>t.value){
- t.right=remove(x,t.right);
- }elseif(t.left!=null&&t.right!=null)//左右节点均不空
- {
- t.value=findmin(t.right).value;//找到右侧最小值替代
- t.right=remove(t.value,t.right);
- }else//左右单空或者左右都空
- {
- if(t.left==null&&t.right==null){
- t=null;
- }elseif(t.right!=null){
- t=t.right;
- }elseif(t.left!=null){
- t=t.left;
- }
- returnt;
- }
- returnt;
- }
完整代码
这个完整代码是笔者在大三时候写的,可能有不少疏漏或者不规范的地方,仅供学习参考,如有疏漏错误还请指正。
二叉排序树完整代码为:
结语
这里我们学习了解了树、二叉树、以及二叉搜素树,对于二叉搜素树插入查找比较容易理解,但是实现的时候要注意函数参数的引用等等。
偏有难度的是二叉树的删除,利用一个递归的思想,分类讨论待删除情况,要找到特殊情况和普通情况,递归一定程度也是问题的转化(转成自己相同问题,作用域减小)需要思考。
下面还会介绍二叉树的三序遍历(递归和非递归)和层序遍历。这些都是比较经典热门的问题需要深入了解。
原文地址.:https://mp.weixin.qq.com/s/pAsk3vmM5Uy2ncZbb5uk8g