本文实例讲述了PHP实现绘制二叉树图形显示功能。分享给大家供大家参考,具体如下:
前言:
最近老师布置了一个作业:理解并实现平衡二叉树和红黑树,本来老师是说用C#写的,但是我学的C#基本都还给老师了,怎么办?那就用现在最熟悉的语言PHP来写吧!
有一个问题来了,书上在讲解树的时候基本上会给出形象的树形图。但是当我们自己试着实现某种树,在调试、输出的时候确只能以字符的形式顺序地输出。这给调试等方面带来了很大的不便。然后在各种百度之后,我发现利用PHP实现二叉树的图形显示的资源几乎是零!好吧,那我就自己个儿实现一个!
效果显示:
如果我是直接在这一步摆代码的话,估计大家会比较烦闷,那我就直接上结果吧,后面在补代码,先激发激发大家的阅读兴趣:
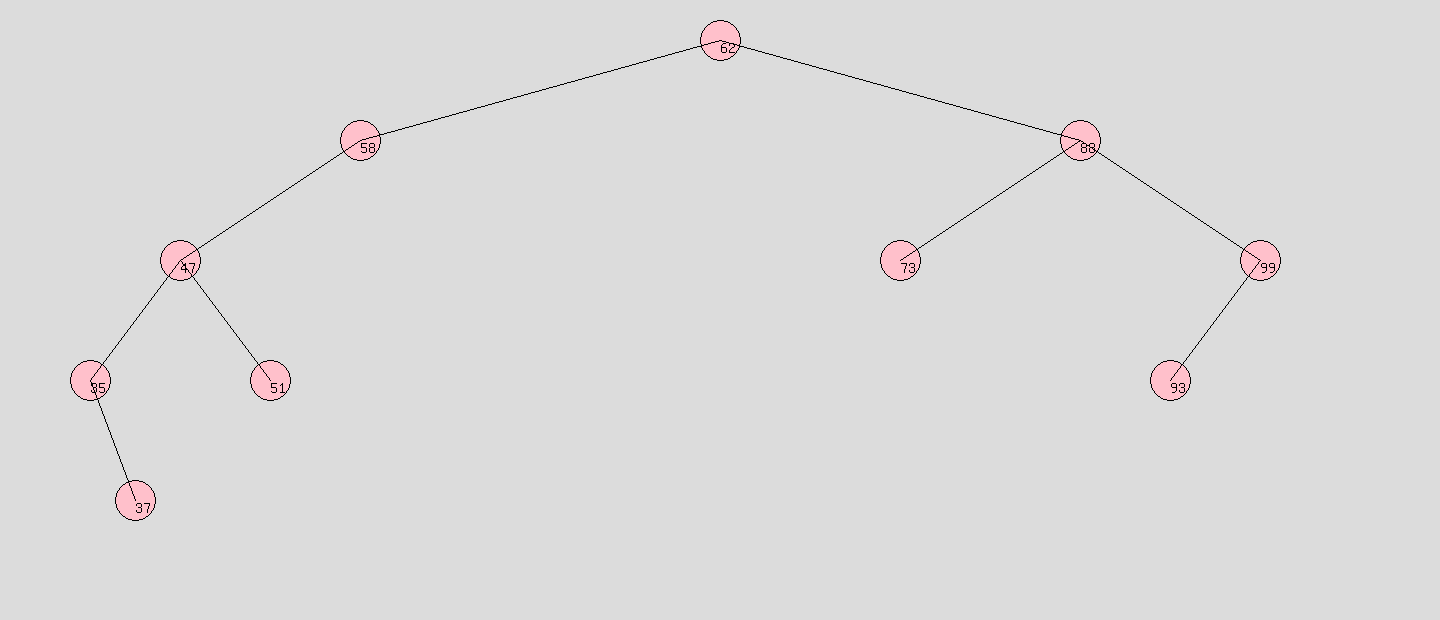
1、搜索二叉树:
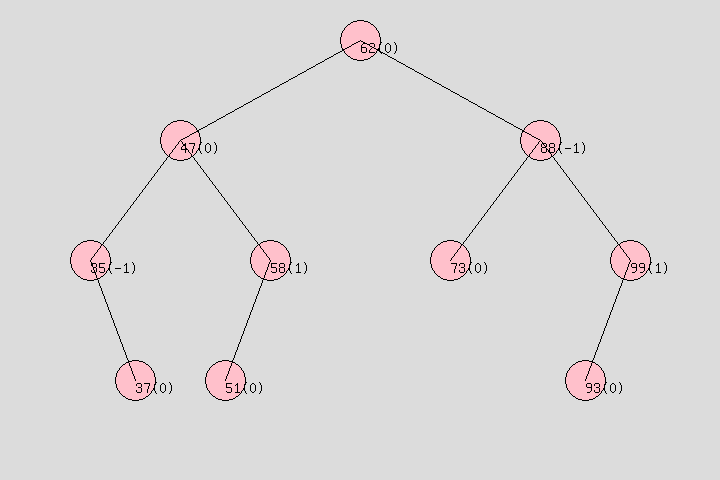
2、平衡二叉树:
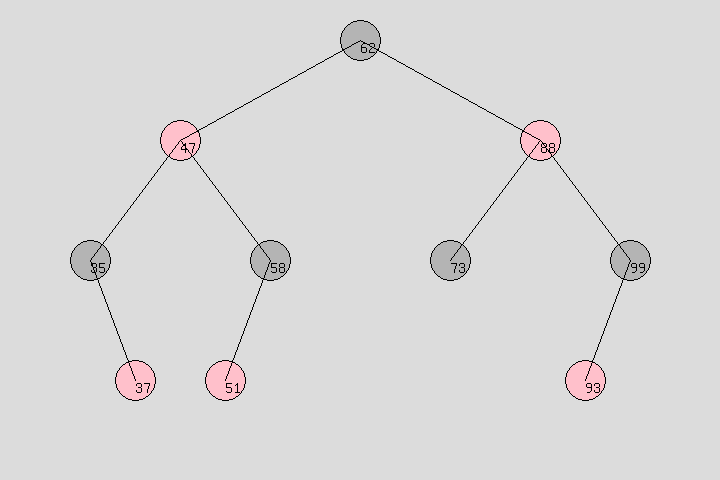
3、红黑树:
上代码:
我们给图片创建一个类吧,显得稍微的小高级:
image.php 文件:
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
|
<?php
/**
* author:LSGOZJ
* description: 绘制二叉树图像
*/
class image
{
//树相关设置
//每层之间的间隔高度
private $level_high = 100;
//最底层叶子结点之间的宽度
private $leaf_width = 50;
//结点圆的半径
private $rad = 20;
//根节点离边框顶端距离
private $leave = 20;
//树(保存树对象的引用)
private $tree;
//树的层数
private $level;
//完全二叉树中最底层叶子结点数量(计算图像宽度时用到,论如何实现图片大小自适应)
private $maxCount;
//图像相关设置
//画布宽度
private $width;
//画布高度
private $height;
//画布背景颜色(RGB)
private $bg = array(
220, 220, 220
);
//节点颜色(搜索二叉树和平衡二叉树时用)
private $nodeColor = array(
255, 192, 203
);
//图像句柄
private $image;
/**
* 构造函数,类属性初始化
* @param $tree 传递一个树的对象
* @return null
*/
public function __construct($tree)
{
$this->tree = $tree;
$this->level = $this->getLevel();
$this->maxCount = $this->GetMaxCount($this->level);
$this->width = ($this->rad * 2 * $this->maxCount) + $this->maxCount * $this->leaf_width;
$this->height = $this->level * ($this->rad * 2) + $this->level_high * ($this->level - 1) + $this->leave;
//1.创建画布
$this->image = imagecreatetruecolor($this->width, $this->height); //新建一个真彩色图像,默认背景是黑色
//填充背景色
$bgcolor = imagecolorallocate($this->image, $this->bg[0], $this->bg[1], $this->bg[2]);
imagefill($this->image, 0, 0, $bgcolor);
}
/**
* 返回传进来的树对象对应的完全二叉树中最底层叶子结点数量
* @param $level 树的层数
* @return 结点数量
*/
function GetMaxCount($level)
{
return pow(2, $level - 1);
}
/**
* 获取树对象的层数
* @param null
* @return 树的层数
*/
function getLevel()
{
return $this->tree->Depth();
}
/**
* 显示二叉树图像
* @param null
* @return null
*/
public function show()
{
$this->draw($this->tree->root, 1, 0, 0);
header("Content-type:image/png");
imagepng($this->image);
imagedestroy($this->image);
}
/**
* (递归)画出二叉树的树状结构
* @param $root,根节点(树或子树) $i,该根节点所处的层 $p_x,父节点的x坐标 $p_y,父节点的y坐标
* @return null
*/
private function draw($root, $i, $p_x, $p_y)
{
if ($i <= $this->level) {
//当前节点的y坐标
$root_y = $i * $this->rad + ($i - 1) * $this->level_high;
//当前节点的x坐标
if (!is_null($parent = $root->parent)) {
if ($root == $parent->left) {
$root_x = $p_x - $this->width / (pow(2, $i));
} else {
$root_x = $p_x + $this->width / (pow(2, $i));
}
} else {
//根节点
$root_x = (1 / 2) * $this->width;
$root_y += $this->leave;
}
//画结点(确定所画节点的类型(平衡、红黑、排序)和方法)
$method = 'draw' . get_class($this->tree) . 'Node';
$this->$method($root_x, $root_y, $root);
//将当前节点和父节点连线(黑色线)
$black = imagecolorallocate($this->image, 0, 0, 0);
if (!is_null($parent = $root->parent)) {
imageline($this->image, $p_x, $p_y, $root_x, $root_y, $black);
}
//画左子节点
if (!is_null($root->left)) {
$this->draw($root->left, $i + 1, $root_x, $root_y);
}
//画右子节点
if (!is_null($root->right)) {
$this->draw($root->right, $i + 1, $root_x, $root_y);
}
}
}
/**
* 画搜索二叉树结点
* @param $x,当前节点的x坐标 $y,当前节点的y坐标 $node,当前节点的引用
* @return null
*/
private function drawBstNode($x, $y, $node)
{
//节点圆的线颜色
$black = imagecolorallocate($this->image, 0, 0, 0);
$nodeColor = imagecolorallocate($this->image, $this->nodeColor[0], $this->nodeColor[1], $this->nodeColor[2]);
//画节点圆
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
//节点圆颜色填充
imagefill($this->image, $x, $y, $nodeColor);
//节点对应的数字
imagestring($this->image, 4, $x, $y, $node->key, $black);
}
/**
* 画平衡二叉树结点
* @param $x,当前节点的x坐标 $y,当前节点的y坐标 $node,当前节点的引用
* @return null
*/
private function drawAvlNode($x, $y, $node)
{
$black = imagecolorallocate($this->image, 0, 0, 0);
$nodeColor = imagecolorallocate($this->image, $this->nodeColor[0], $this->nodeColor[1], $this->nodeColor[2]);
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
imagefill($this->image, $x, $y, $nodeColor);
imagestring($this->image, 4, $x, $y, $node->key . '(' . $node->bf . ')', $black);
}
/**
* 画红黑树结点
* @param $x,当前节点的x坐标 $y,当前节点的y坐标 $node,当前节点的引用
* @return null
*/
private function drawRbtNode($x, $y, $node)
{
$black = imagecolorallocate($this->image, 0, 0, 0);
$gray = imagecolorallocate($this->image, 180, 180, 180);
$pink = imagecolorallocate($this->image, 255, 192, 203);
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
if ($node->IsRed == TRUE) {
imagefill($this->image, $x, $y, $pink);
} else {
imagefill($this->image, $x, $y, $gray);
}
imagestring($this->image, 4, $x, $y, $node->key, $black);
}
}
|
好,现在我们来看看在客户端如何调用:
client.php
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Client
{
public static function Main()
{
try {
//实现文件的自动加载
function autoload($class)
{
include strtolower($class) . '.php';
}
spl_autoload_register('autoload');
$arr = array(62, 88, 58, 47, 35, 73, 51, 99, 37, 93);
// $tree = new Bst(); //搜索二叉树
$tree = new Avl(); //平衡二叉树
// $tree = new Rbt(); //红黑树
$tree->init($arr); //树的初始化
// $tree->Delete(62);
// $tree->Insert(100);
// $tree->MidOrder(); //树的中序遍历(这也是调试的一个手段,看看数字是否从小到大排序)
$image = new image($tree);
$image->show(); //显示图像
} catch (Exception $e) {
echo $e->getMessage();
}
}
}
Client::Main();
|
这里用到的那三个树的类如下:
二叉搜索树bst.php:
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
|