ios 的坐标系和我们几何课本中的二维坐标系并不一样！
使用 uibezierpath 进行绘制圆弧的方法，通常会直接使用 addarc ：
?
|
1
|
addarc(withcenter:, radius:, startangle:, endangle:, clockwise:)
|
或者使用 addcurve 进行拟圆弧：
?
|
1
|
addcurve(to:, controlpoint1:, controlpoint2:)
|
其实我们可以通过，两个坐标点(startpoint & endpoint)，和两点间的线段对应的圆弧的弧度(angle/radian)就能确定这个圆的信息(半径radius, center)， 所以我们是不是可以封装出只提供 start, end 和 angle 就能绘制 arc 的函数？
?
|
1
|
addarc(startpoint: , endpoint: , angle: , clockwise:)
|
# 计算两点间的距离
这里逻辑很简单不做赘述。
?
|
1
2
3
4
5
|
func calculatelinelength(_ point1: cgpoint, _ point2: cgpoint) -> cgfloat {
let w = point1.x - point2.x
let h = point1.y - point2.y
return sqrt(w * w + h * h)
}
|
# 计算两点间的夹角
计算 point 和 origin 连线在 ios 坐标系的角度
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func calculateangle(point: cgpoint, origin: cgpoint) -> double {
if point.y == origin.y {
return point.x > origin.x ? 0.0 : -double.pi
}
if point.x == origin.x {
return point.y > origin.y ? double.pi * 0.5 : double.pi * -0.5
}
// note: 修正标准坐标系角度到 ios 坐标系
let rotationadjustment = double.pi * 0.5
let offsetx = point.x - origin.x
let offsety = point.y - origin.y
// note: 使用 -offsety 是因为 ios 坐标系与标准坐标系的区别
if offsety > 0 {
return double(atan(offsetx / -offsety)) + rotationadjustment
} else {
return double(atan(offsetx / -offsety)) - rotationadjustment
}
}
|
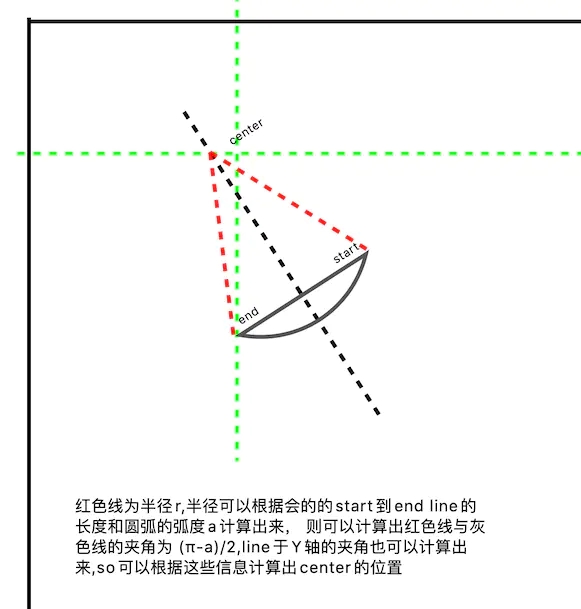
# 计算圆心的坐标
如果你已经将几何知识丢的差不多了的话，我在这里画了个大概的草图，如下( angle 比较小时)：
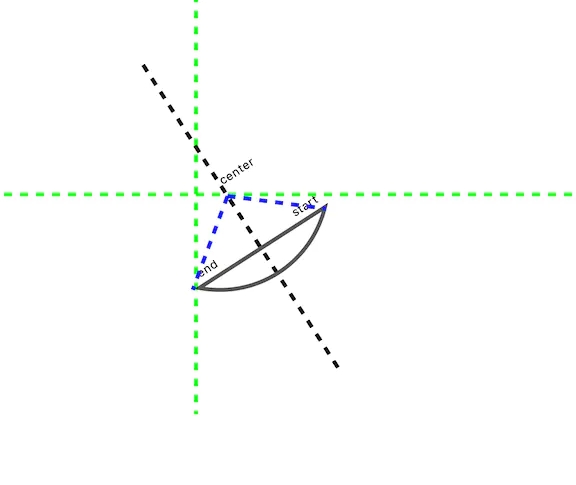
angle 比较大时：
所以我么可以写出如下计算中心点的代码
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
// woring: 只计算从start到end **顺时针** 计算对应的 **小于π** 圆弧对应的圆心
// note: 计算逆时针(end到start)可以看做将传入的start和end对调后计算顺时针时的圆心位置
// note: 计算大于π的叫相当于将end和start对换后计算2π-angle的顺时针圆心位置
// note: 综上传入start，end，angle 右外部自行处理逻辑
func calculatecenterfor(startpoint start: cgpoint, endpoint end: cgpoint, radian: double) -> cgpoint {
guard radian <= double.pi else {
fatalerror("does not support radian calculations greater than π!")
}
guard start != end else {
fatalerror("start position and end position cannot be equal!")
}
if radian == double.pi {
let centerx = (end.x - start.x) * 0.5 + start.x
let centery = (end.y - start.y) * 0.5 + start.y
return cgpoint(x: centerx, y: centery)
}
let lineab = calculatelinelength(start, end)
// 平行 y 轴
if start.x == end.x {
let centery = (end.y - start.y) * 0.5 + start.y
let tanresult = cgfloat(tan(radian * 0.5))
let offsetx = lineab * 0.5 / tanresult
let centerx = start.x + offsetx * (start.y > end.y ? 1.0 : -1.0)
return cgpoint(x: centerx, y: centery)
}
// 平行 x 轴
if start.y == end.y {
let centerx = (end.x - start.x) * 0.5 + start.x
let tanresult = cgfloat(tan(radian * 0.5))
let offsety = lineab * 0.5 / tanresult
let centery = start.y + offsety * (start.x < end.x ? 1.0 : -1.0)
return cgpoint(x: centerx, y: centery)
}
// 普通情况
// 计算半径
let radius = lineab * 0.5 / cgfloat(sin(radian * 0.5))
// 计算与 y 轴的夹角
let angletoyaxis = atan(abs(start.x - end.x) / abs(start.y - end.y))
let cacluteangle = cgfloat(double.pi - radian) * 0.5 - angletoyaxis
// 偏移量
let offsetx = radius * sin(cacluteangle)
let offsety = radius * cos(cacluteangle)
var centetx = end.x
var centery = end.y
// 以 start 为原点判断象限区间(ios坐标系)
if end.x > start.x && end.y < start.y {
// 第一象限
centetx = end.x + offsetx
centery = end.y + offsety
} else if end.x > start.x && end.y > start.y {
// 第二象限
centetx = start.x - offsetx
centery = start.y + offsety
} else if end.x < start.x && end.y > start.y {
// 第三象限
centetx = end.x - offsetx
centery = end.y - offsety
} else if end.x < start.x && end.y < start.y {
// 第四象限
centetx = start.x + offsetx
centery = start.y - offsety
}
return cgpoint(x: centetx, y: centery)
}
|
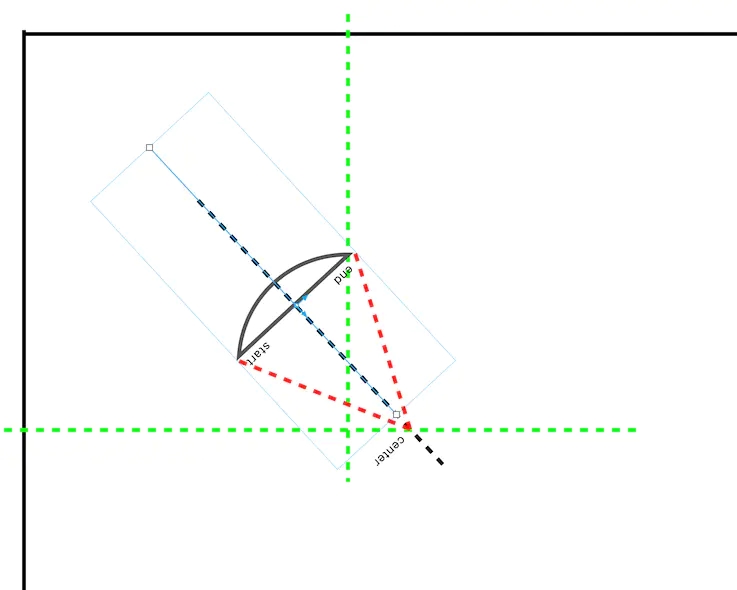
这里附上一个逆时针绘制第一张图中圆心位置的草图，图中已将 start 和 end 对换
如果你对其中计算时到底该使用 + 还是 – 有困惑的话也可以自己多画些草图大概验证下，总之有疑惑多动手
相关文章
猜你喜欢
- ASP.NET自助建站系统的数据库备份与恢复操作指南 2025-06-10
- 个人网站服务器域名解析设置指南：从购买到绑定全流程 2025-06-10
- 个人网站搭建：如何挑选具有弹性扩展能力的服务器？ 2025-06-10
- 个人服务器网站搭建：如何选择适合自己的建站程序或框架？ 2025-06-10
- 64M VPS建站：能否支持高流量网站运行？ 2025-06-10
