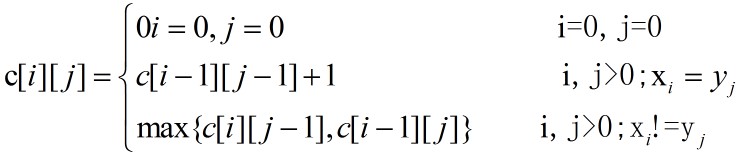Java算法之最长公共子序列问题(LCS)实例分析

本文实例讲述了java算法之最长公共子序列问题(lcs)。分享给大家供大家参考，具体如下：

问题描述：一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说，若给定序列x= { x1, x2,…, xm}，则另一序列z= {z1, z2,…, zk}是x的子序列是指存在一个严格递增的下标序列 {i1, i2,…, ik}，使得对于所有j=1,2,…,k有 xij=zj。例如，序列z={b,c,d,b}是序列x={a,b,c,b,d,a,b}的子序列，相应的递增下标序列为{2,3,5,7}。给定两个序列x和y，当另一序列z既是x的子序列又是y的子序列时，称z是序列x和y的公共子序列。例如，若x= { a, b, c, b, d, a, b}和y= {b, d, c, a, b, a}，则序列{b,c,a}是x和y的一个公共子序列，序列{b,c,b,a}也是x和y的一个公共子序列。而且，后者是x和y的一个最长公共子序列，因为x和y没有长度大于4的公共子序列。给定两个序列x= {x1, x2, …, xm}和y= {y1, y2, … , yn}，要求找出x和y的一个最长公共子序列。

问题解析：设x= { a, b, c, b, d, a, b},y= {b, d, c, a, b, a}。求x，y的最长公共子序列最容易想到的方法是穷举法。对x的多有子序列，检查它是否也是y的子序列，从而确定它是否为x和y的公共子序列。由集合的性质知，元素为m的集合共有2^m个不同子序列，因此，穷举法需要指数级别的运算时间。进一步分解问题特性，最长公共子序列问题实际上具有最优子结构性质。

设序列x={x1,x2,……xm}和y={y1,y2,……yn}的最长公共子序列为z={z1,z2,……zk}。则有：

(1)若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。
(2)若xm!=yn且zk!=xm，则z是xm-1和y的最长公共子序列。
(3)若xm!=yn且zk!=yn，则z是x和yn-1的最长公共子序列。
其中，xm-1={x1,x2……xm-1}，yn-1={y1,y2……yn-1},zk-1={z1,z2……zk-1}。

递推关系：用c[i][j]记录序列xi和yj的最长公共子序列的长度。其中，xi={x1,x2……xi}，yj={y1,y2……yj}。当i=0或j=0时，空序列是xi和yj的最长公共子序列。此时，c[i][j]=0；当i,j>0，xi=yj时，c[i][j]=c[i-1][j-1]+1；当i,j>0，xi!=yj时，
c[i][j]=max{c[i][j-1],c[i-1][j]}，由此建立递推关系如下：

构造最优解：由以上分析可知，要找出x={x1,x2,……xm}和y={y1,y2,……yn}的最长公共子序列,可以按一下方式递归进行：当xm=yn时，找出xm-1和yn-1的最长公共子序列，然后在尾部加上xm(=yn)即可得x和y的最长公共子序列。当xm!=yn时，必须解两个子问题，即找出xm-1和y的一个最长公共子序列及x和yn-1的一个最长公共子序列。这两个公共子序列中较长者为x和y的最长公共子序列。设数组b[i][j]记录c[i][j]的值由哪一个子问题的解得到的，从b[m][n]开始，依其值在数组b中搜索，当b[i][j]=1时，表示xi和yj的最长公共子序列是由xi-1和yj-1的最长公共子序列在尾部加上xi所得到的子序列。当b[i][j]=2时，表示xi和yj的最长公共子序列与xi-1和yj-1的最长公共子序列相同。当b[i][j]=3时，表示xi和yj的最长公共子序列与xi和yj-1的最长公共子序列相同。