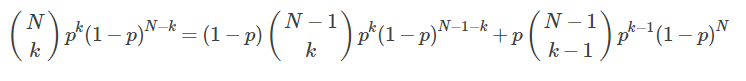本文研究的主要内容是java编程二项分布的递归和非递归实现,具体如下。
问题来源:
算法第四版 第1.1节 习题27:return (1.0 – p) * binomial(n – 1, k, p) + p * binomial(n – 1, k – 1, p);
计算递归调用次数,这里的递归式是怎么来的?
二项分布:
定义:n个独立的是/非试验中成功次数k的离散概率分布,每次实验成功的概率为p,记作b(n,p,k)。
概率公式:p(ξ=k)= c(n,k) * p^k * (1-p)^(n-k)
其中c(n, k) = (n-k) !/(k! * (n-k)!),记作ξ~b(n,p),期望:eξ=np,方差:dξ=npq,其中q=1-p。
概率统计里有一条递归公式:
这个便是题目中递归式的来源。
该递推公式来自:c(n,k)=c(n-1,k)+c(n-1,k-1)。实际场景是从n个人选k个,有多少种组合?将着n个人按1~n的顺序排好,假设第k个人没被选中,则需要从剩下的n-1个人中选k个;第k个选中了,则需要从剩下的n-1个人中选k-1个。
|
1
2
3
4
5
6
7
8
9
10
|
public static double binomial(int n, int k, double p) {
count++; //记录递归调用次数
if (n == 0 && k == 0) {
return 1.0;
}
if (n < 0 || k < 0) {
return 0.0;
}
return (1.0 - p) * binomial(n - 1, k, p) + p * binomial(n - 1, k - 1, p);
}
|
实验结果:
|
1
2
3
4
|
n k p 调用次数
10 5 0.25 2467
20 10 0.25 2435538
30 15 0.25 2440764535
|
由结果可以看出来这个递归方法需要调用的次数呈几何灾难,n到50就算不下去了。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
private static long count = 0;
private static double[][] m;
private static double binomial(int n, int k, double p) {
count++;
if (n == 0 && k == 0) {
return 1.0;
}
if (n < 0 || k < 0) {
return 0.0;
}
if (m[n][k] == -1) { //将计算结果存起来,已经计算过的直接拿过来用,无需再递归计算
m[n][k] = (1.0 - p) * binomial(n - 1, k, p) + p * binomial(n - 1, k - 1, p);
}
return m[n][k];
}
public static double binomial(int n, int k, double p) {
m = new double[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= k; j++) {
m[i][j] = -1;
}
}
return binomial(n, k, p);
}
|
实验结果:
|
1
2
3
4
5
6
|
n k p 调用次数
10 5 0.25 101
20 10 0.25 452
30 15 0.25 1203
50 25 0.25 3204
100 50 0.25 5205
|
由实验结果可以看出调用次数大幅减小,算法可以使用。
事实上,不利用递归,直接计算组合数和阶乘,反而速度更快。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
//计算组合数
public static double combination(double n, double k)
{
double min = k;
double max = n-k;
double t = 0;
double nn=1;
double kk=1;
if(min>max){
t=min;
min = max;
max=t;
}
while(n>max){//分母中较大的那部分阶乘约分不用计算
nn=nn*n;
n--;
}
while(min>0){//计算较小那部分的阶乘
kk=kk*min;
min--;
}
return nn/kk;
}
//计算二项分布值
public static double binomial(int n,int k,double p)
{
double a=1;
double b=1;
double c =combination(n,k);
while((n-k)>0){ //计算(1-p)的(n-k)次方
a=a*(1-p);
n--;
}
while(k>0){ //计算p的k次方
b=b*p;
k--;
}
return c*a*b;
}
|
实验结果:
|
1
2
3
4
|
n k p 二项分布值
10, 5, 0.25 0.058399200439453125
20, 10, 0.25 0.009922275279677706
50, 25, 0.25 8.44919466990397e-5
|
与前面的算法比对,计算结果是正确的,而且运行速度是非常之快的。
总结
以上就是本文关于java编程二项分布的递归和非递归实现代码实例的全部内容,希望对大家有所帮助。感兴趣的朋友可以继续参阅本站其他相关专题,如有不足之处,欢迎留言指出。感谢朋友们对本站的支持!
原文链接:http://blog.csdn.net/u014485485/article/details/77506844
相关文章
- 个人网站服务器域名解析设置指南:从购买到绑定全流程 2025-06-10
- 个人网站搭建:如何挑选具有弹性扩展能力的服务器? 2025-06-10
- 个人服务器网站搭建:如何选择适合自己的建站程序或框架? 2025-06-10
- 64M VPS建站:能否支持高流量网站运行? 2025-06-10
- 64M VPS建站:怎样选择合适的域名和SSL证书? 2025-06-10
- 2025-07-10 怎样使用阿里云的安全工具进行服务器漏洞扫描和修复?
- 2025-07-10 怎样使用命令行工具优化Linux云服务器的Ping性能?
- 2025-07-10 怎样使用Xshell连接华为云服务器,实现高效远程管理?
- 2025-07-10 怎样利用云服务器D盘搭建稳定、高效的网站托管环境?
- 2025-07-10 怎样使用阿里云的安全组功能来增强服务器防火墙的安全性?
快网idc优惠网
QQ交流群
-
2025-06-04 82
-
2025-05-25 75
-
2025-05-27 81
-
2025-05-25 45
-
2025-05-25 0