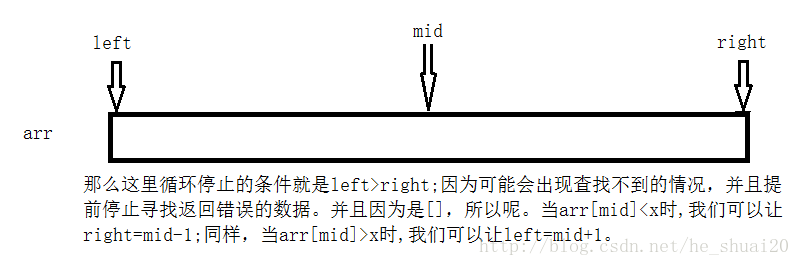
C++ 中二分查找递归非递归实现并分析

C++ 中二分查找递归非递归实现并分析

二分查找在有序数列的查找过程中算法复杂度低，并且效率很高。因此较为受我们追捧。其实二分查找算法，是一个很经典的算法。但是呢，又容易写错。因为总是考虑不全边界问题。

用非递归简单分析一下，在编写过程中，如果编写的是以下的代码：

#include<iostream>

#include<assert.h>

using namespace std;

int binaty_search(int* arr, size_t n, int x)

{

assert(arr);

int left = 0;

int right = n - 1;

while (left <= right)

{

int mid = (left + right) / 2;

if (x < arr[mid])

{

right = mid-1;

}

else if (x > arr[mid])

{

left = mid+1;

}

else

return mid;

}

return -1;

}

int main()

{

int arr[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 0) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 1) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 2) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 3) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 4) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 5) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 6) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 7) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 8) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 9) << endl;

cout << binaty_search(arr, sizeof(arr) / sizeof(int), 10) << endl;

return 0;

}

那么我们可以简单分析一下：

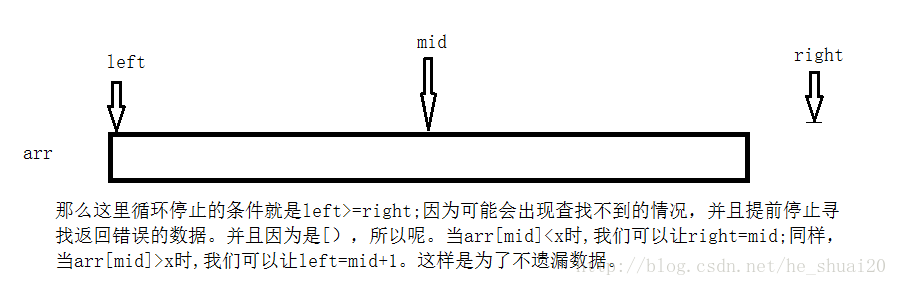
如果是以下这样的代码实现：

#include<iostream>

#include<assert.h>

using namespace std;

int binaty_search(int* arr, size_t n, int x)

{

assert(arr);

int left = 0;

int right = n;

while (left < right)

{

int mid = (left + right) / 2;

if (x < arr[mid])

{

right = mid;

}

else if (x > arr[mid])

{

left = mid + 1;