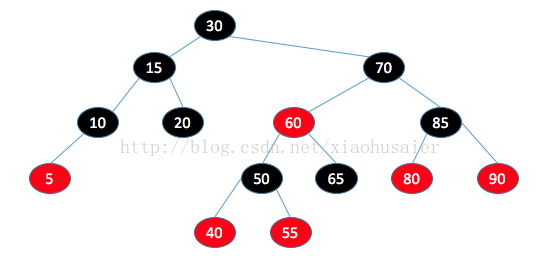
红黑树是具有下列着色性质的二叉查找树:
1.每一个节点或者着红色,或者着黑色。
2.根是黑色的。
3.如果一个节点是红色的,那么它的子节点必须是黑色。
4.从一个节点到一个NULL指针的每一条路径必须包含相同数目的黑色节点。
下面是一棵红黑树。
1.自底向上插入
通常把新项作为树叶放到树中。如果我们把该项涂成黑色,那么违反条件4,因为将会建立一条更长的黑节点路径。因此这一项必须涂成红色。如果它的父节点是黑色的,插入完成。如果父节点是红色的,那么违反条件3。在这种情况下我们必须调整该树以满足条件3。用于完成这项目任务的基本操作是颜色的改变和树的旋转。
如果新插入的节点的父节点是黑色,那么插入完成。
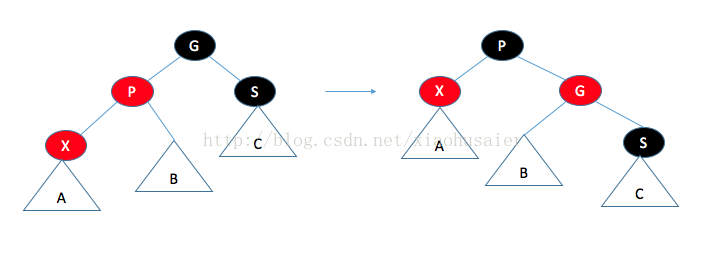
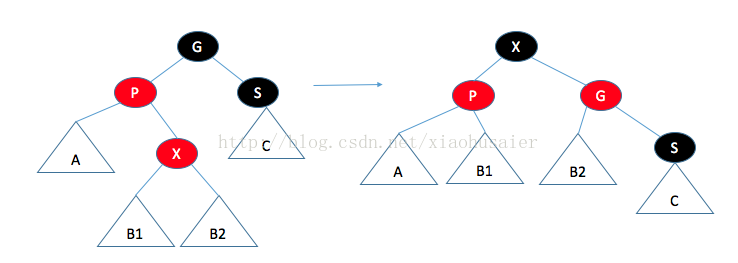
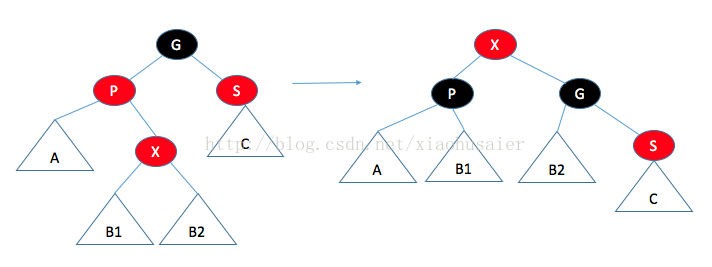
如果父节点是红色,那么有几种情形需要考虑。首先,假设这个父节点的兄弟是黑色(NULL节点约定为黑色)。这对于插入3或8是适用的,但对插入99不适用。令X是新加的树叶,P是它的父节点,S是该父节点的兄弟,G是祖父节点情况一:父节点的兄弟是黑色的。通过操作使得到达A,B,C的黑色路径保持不变(满足条件4),而且没有连续的红色节点(满足条件3).。
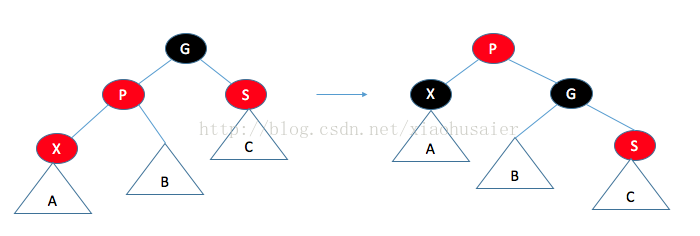
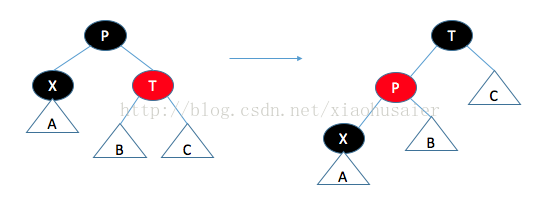
情况二:父节点的兄弟是红色的。
2.自顶向下删除
红黑树中的删除可以是自顶向下进行。每一件工作都归结于能够删除一片树叶。这是因为,要删除一个带有两个儿子的节点,我们用右子树上的最小节点代替它;该节点最多有一个儿子,然后将该节点删除。只有一个右儿子的节点可以用相同的方式删除,而只有一个左儿子的节点通过用其左子树上最大的节点替换,然后可将该节点删除。但是假如删除的节点不是红色的,那么就会破坏红黑树的平衡。解决的方法就是保证从上到下删除期间树叶是红色的。
在整个讨论中,令X为当前节点,T是它的兄弟,而P是它们的父亲。开始时我们把根涂成红色。当沿着树向下遍历时,我们设法保证X是红色的。当我们到达一个新的节点时,我们要确信P是红色的并且X和T是黑色的(因为不能有两个相连的红色节点)。存在两种主要情形。
情况一:X有两个黑色儿子。此时有三个子情况。
(1)T有两个黑儿子,那么我们可以翻转X、T、P的颜色来保持这种不变性。
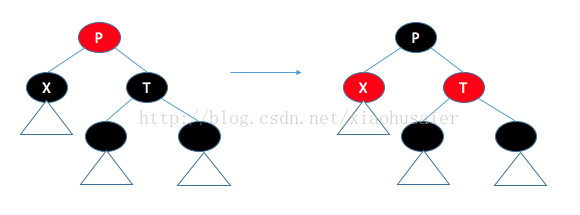

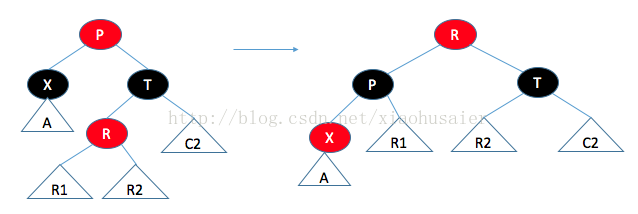
(2)T的左儿子是红色的

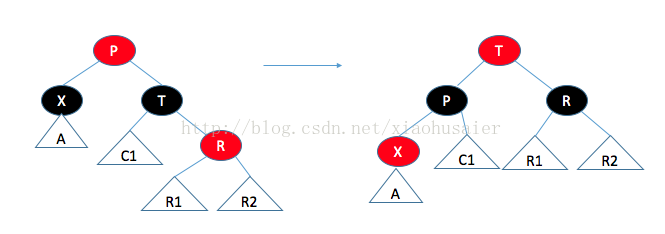
(3)T的右儿子是红色的

情况二:X的儿子之一是红的。在这种情况下,我们落到下一层,得到新的X、T、P。如果幸运,X落在红儿子上。则我们继续前行。如果不是这样,那么我们知道T将是红的,而X和P将是黑的。我们可以旋转T和P,使得X的新父亲是红的;当然X和它的祖父是黑的。此时我们可以回到第一种主情况。

3.红黑树的实现
3.1 头文件