C语言手把手教你实现贪吃蛇AI（中）

也想出现在这里？点击联系我~

手把手教你实现贪吃蛇AI，具体内容如下

1. 目标

这一部分主要是讲解编写贪吃蛇AI所需要用到的算法基础。

2. 问题分析

贪吃蛇AI说白了就是寻找一条从蛇头到食物的一条最短路径，同时这条路径需要避开障碍物，这里仅有的障碍就是蛇身。而A star 算法就是专门针对这一个问题的。在A star 算法中需要用到排序算法，这里采用堆排序（当然其他排序也可以），如果对堆排序不熟悉的朋友，请移步到这里——堆排序，先看看堆排序的内容。

3. A*算法

A star(也称A*)搜寻算法俗称A星算法。这是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。常用于游戏中对象的移动计算上。A* 算法是一种启发式搜寻算法，有别于DFS， BFS搜索。可以这样理解“启发式”的涵义，比如从起点A到达目的地B的路线，并不是直接告诉你，从A出发，向东行驶200米，右转进入XX路，直行500米到达B；而是从A出发，直行，直到遇到第一家肯德基，右转直到看到B大厦。而A*算法中用来启发的线索就是移动成本，也就是权重。

3.1 移动成本

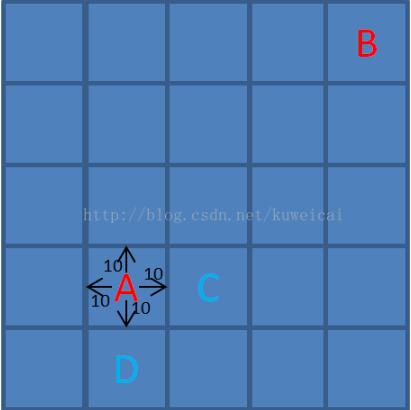
如下图所示，从A点出发，可以有四个方向可走（由于贪吃蛇仅仅可以走上下左右四个方向，所以这里不考虑走斜线的情况），假设每个方向移动一格的成本为10，A*算法中采用的F值来评价移动成本，F=G+H。假设节点C是待考察的一个点，G代表的是从起点A到C的移动成本，如下图的情况G=10。那么H代表的就是从C点到目标B点的移动代价的预估值，如下图的情况H=50，那么F=60。为什么说是预估，因为现在对于从C点到B点的情况还不清楚，因为中间可能存在障碍物，那么实际的移动代价就会大于预估的情况。而对于待考察点D，其F=80，显然在C 和D点中（当然这里待考察的点不止C和D点），A*算法会选择C点。

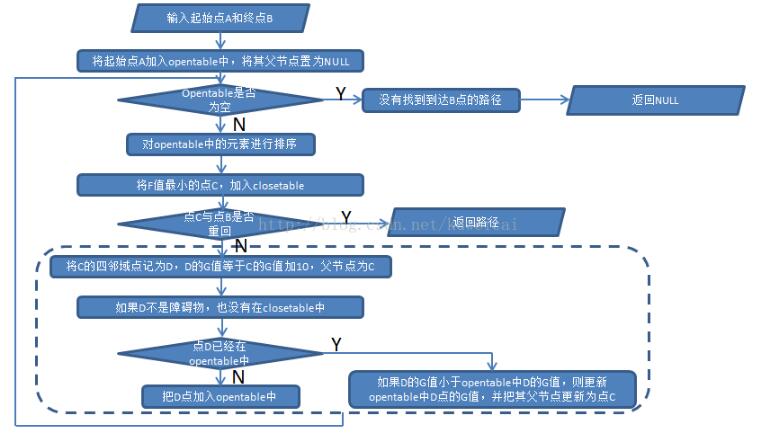
3.2 算法流程图

4. 源代码

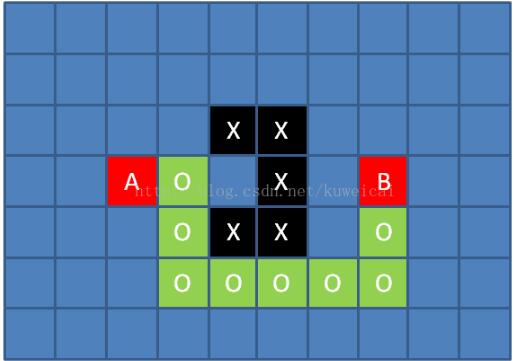
代码中假定起始点A(5,10)，食物B(5,15)，如下图。其中‘X'代表障碍物，‘O'代表的就是寻找到的从A到B的路径。