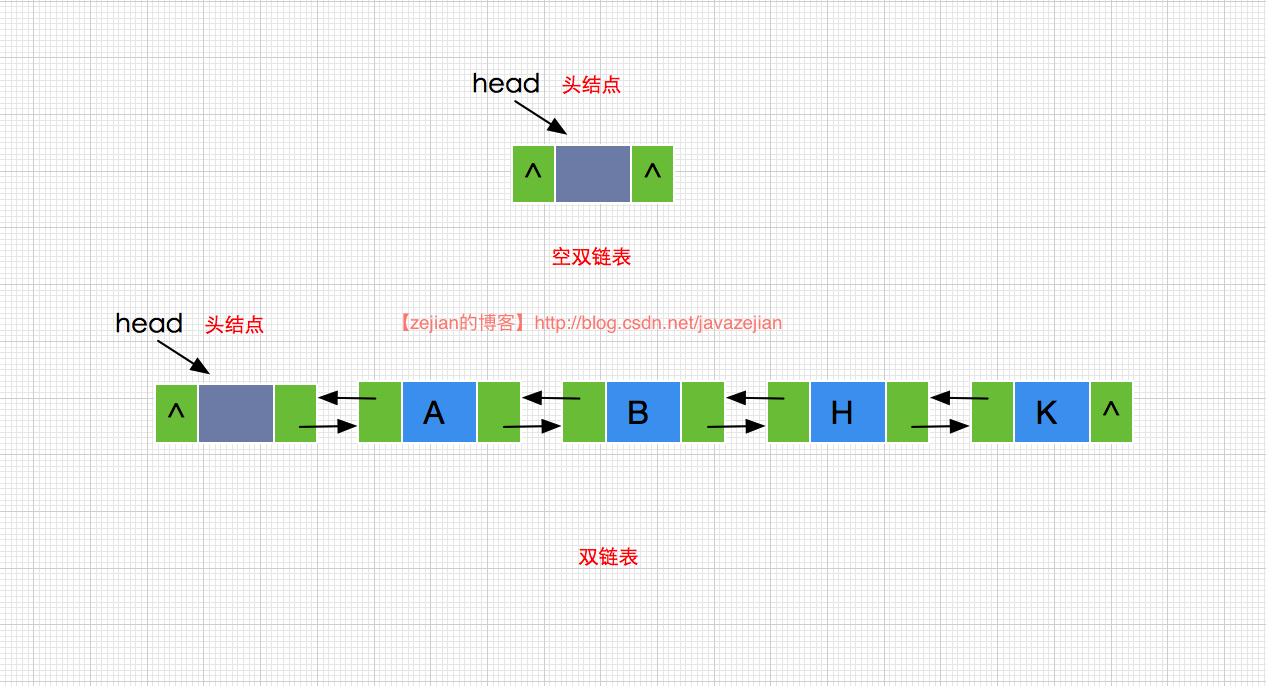
在单链表分析中，我们可以知道每个结点只有一个指向后继结点的next域，倘若此时已知当前结点p，需要查找其前驱结点，那么就必须从head头指针遍历至p的前驱结点，操作的效率很低，因此如果p有一个指向前驱结点的next域，那效率就高多了，对于这种一个结点中分别包含了前驱结点域pre和后继结点域next的链表，称之为双链表。本篇我们将从以下结点来分析双链表
双链表的设计与实现
双链表的主要优点是对于任意给的结点，都可以很轻易的获取其前驱结点或者后继结点，而主要缺点是每个结点需要添加额外的next域，因此需要更多的空间开销，同时结点的插入与删除操作也将更加耗时，因为需要更多的指针指向操作。双链表的结构图如下：
创建headdoubleilinkedlist类并实现ilinekedlist接口(和上篇博文的接口一样)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
/**
* created by zejian on 2016/10/23.
* 双链表的实现,带头结点(不带数据)的双链表,为了更高的效率该类包含指向尾部的指针tail
*/
public class headdoubleilinkedlist<t> implements ilinkedlist<t> {
protected dnode<t> head; //不带数据的头结点
protected dnode<t> tail; //指向尾部的指针
public headdoubleilinkedlist(){
//初始化头结点
this.head =this.tail= new dnode<>();
}
//先省略其他代码
........
}
|
结点类结构如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
package com.zejian.structures.linkedlist.doublelinked;
/**
* created by zejian on 2016/10/23.
* 双链表结点
*/
public class dnode<t> {
public t data;
public dnode<t> prev, next;//前继指针和后继指针
public dnode(t data, dnode<t> prev, dnode<t> next)
{
this.data = data;
this.prev = prev;
this.next = next;
}
public dnode(t data)
{
this(data, null, null);
}
public dnode()
{
this(null, null, null);
}
public string tostring()
{
return this.data.tostring();
}
}
|
通过上篇的分析，我们对链表的插入、删除、查找、替换等操作也比较熟悉了，因此针对双链表的实现，主要分析其插入、删除、查找、替换等方法，其他没有分析的看实现源码即可（最后会给出双链表的实现代码）
双链表的插入操作分析与实现
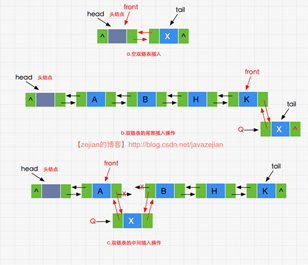
我们先来看看双链表的插入，虽然有不带数据的头结点，但是由于是双向链表，所以在插入双链表时需分两种情况，一种是在插入空双链表和尾部插入，另一种是双链表的中间插入，如下图在空双链表插入值x：
从图可以看出（a）和（b）属于同种情况，需要注意front.next != null的情况，否则就会抛空指针，而（c）的情况属于中间插入无需无需理会front.next != null的条件，因为中间插入时无论如何其后继结点时不会为null的，插入方法的实现代码如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
/**
* 插入结点
* @param index
* @param data
* @return
*/
@override
public boolean add(int index, t data) {
if(index<0||data==null)
throw new nullpointerexception("index < 0 || data == null");
int j = 0;
dnode<t> front = this.head;
//查找要插入结点位置的前一个结点
while (front.next != null && j < index) {
j++;
front = front.next;
}
//创建需要插入的结点,并让其前继指针指向front,后继指针指向front.next
dnode<t> q = new dnode<t>(data, front, front.next);
//空双链表插入和尾部插入，无需此操作
if(front.next != null) {
//更改front.next的前继指针
front.next.prev = q;
}
//更改front的后继指针
front.next = q;
//在尾部插入时需要注意更新tail指向
if(front==this.tail){
this.tail=q;
}
return true;
}
|
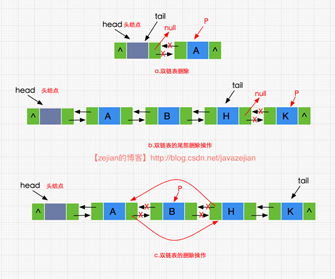
双链表的删除操作分析与实现
双链表的删除操作与插入操作原理上是相似的，我们可以看出（a）（b）是属于同种情况，需要防止 p.next.prev抛空指针的情况，而对于（c）情况则无需关系 p.next.prev的值，删除的具体实现如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
/**
* 根据下标删除结点
* 1.头删除
* 2.中间删除
* 3.尾部删除,更新tail指向
* @param index 下标起始值为0
* @return
*/
@override
public t remove(int index) {
int size=length();
t temp=null;
if(index<0||index>=size||isempty()){
return temp;
}
dnode<t> p=this.head;
int j=0;
//头删除/尾删除/中间删除,查找需要删除的结点(要删除的当前结点因此i<=index)
while (p!=null&&j<=index){
p=p.next;
j++;
}
//当双链表只有一个结点时或尾部删除时,无需此步
if(p.next!=null){
p.next.prev=p.prev;
}
p.prev.next=p.next;
//如果是尾结点
if (p==this.tail) {
this.tail = p.prev;//更新未结点的指向
}
temp=p.data;
return temp;
}
|
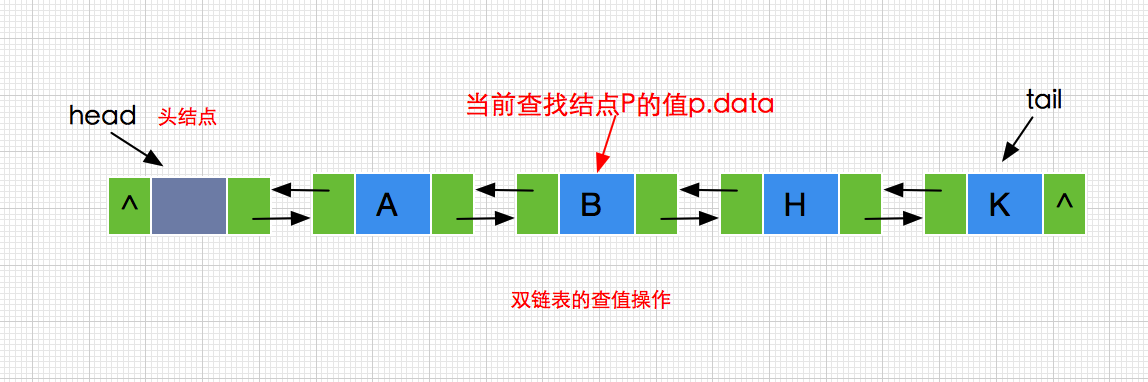
双链表的查值操作分析与实现
双链表的查找值的操作与单链表并没有什么区别，只要找到需要查找的当前结点获取其值即可，如下：
代码实现如下：