定义
红黑树(英语:red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
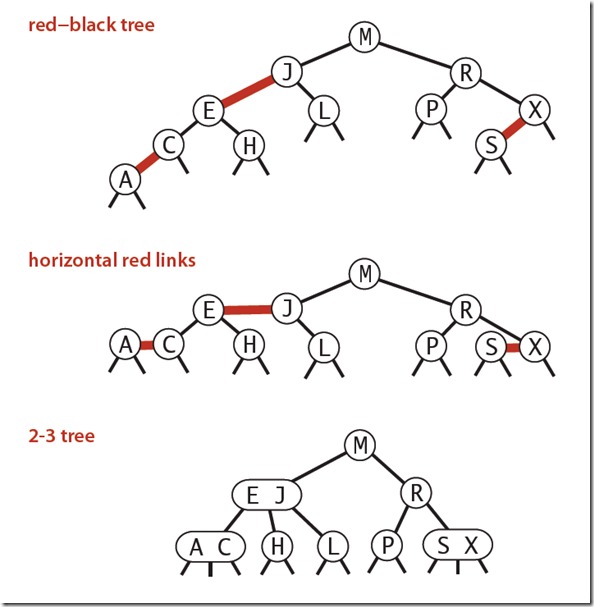
红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树:
红链接均为左链接;没有任何一个结点同时和两条红链接相连;该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
满足这样定义的红黑树和相应的2-3树是一一对应的。
旋转
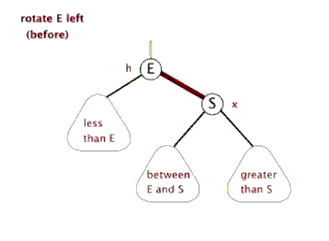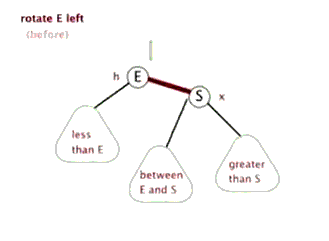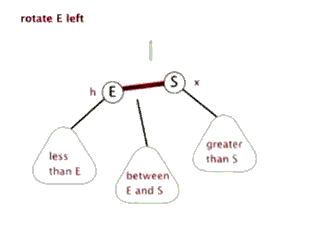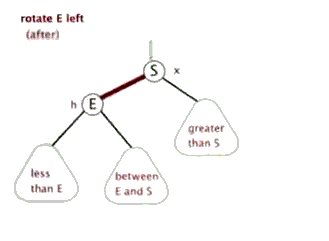
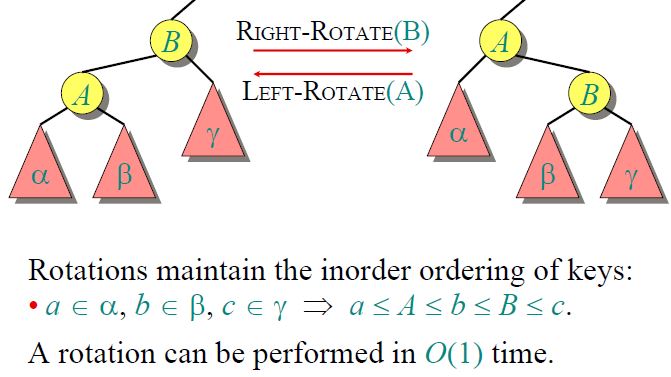
旋转又分为左旋和右旋。通常左旋操作用于将一个向右倾斜的红色链接旋转为向左链接。对比操作前后,可以看出,该操作实际上是将红线链接的两个节点中的一个较大的节点移动到根节点上。
左旋操作如下图:
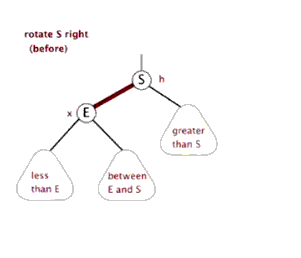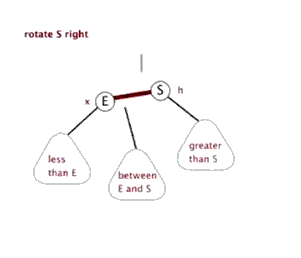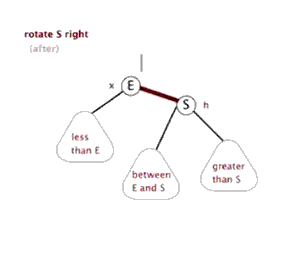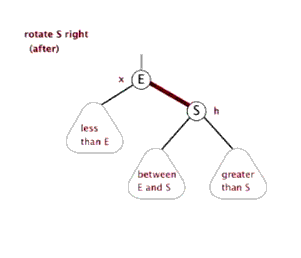
右旋旋操作如下图:
即:
复杂度
红黑树的平均高度大约为lgn。
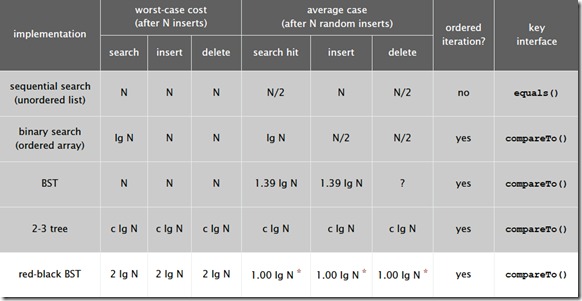
下图是红黑树在各种情况下的时间复杂度,可以看出红黑树是2-3查找树的一种实现,他能保证最坏情况下仍然具有对数的时间复杂度。
java代码