为什么需要树这种结构
1.数组存储方式分析:
- 优点:通过下标方式访问元素,速度快。对于有序数组,还可以使用二分查找提高检索速度。
- 缺点:如果检索某个具体的值,或者插入值(按一定的顺序)会整体移动,效率较低。
2.链式存储方式分析:
- 优点:在一定程度上对数组存储方式优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可,删除效率很高)。
- 缺点:在进行检索时,效率仍然很低,需要从头结点开始遍历。
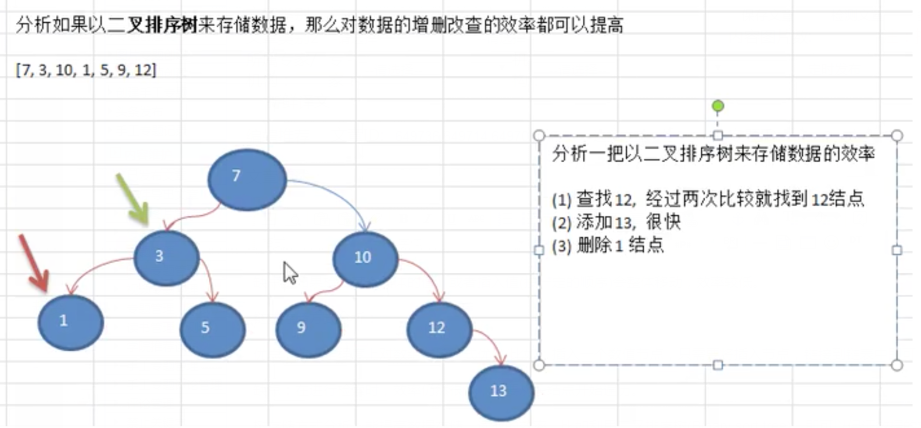
3.树存储方式分析:能提高数据存储,读取的效率,比如利用二叉排序树(Binary sort tree),即可以保证数据的检索速度,同时也可以保证数据的插入、删除、修改的速度。假设一组[7,3,10,1,5,9,12]以树的方式存储,分析如下图:
二叉树的前序遍历、中序遍历、后序遍历
- 前序遍历:输出父节点、输出左边节点、输出右边节点;
- 中序遍历:输出左边节点、输出父节点、输出右边节点;
- 后序遍历:输出左边节点、输出右边节点、输出父节点;
需求案例
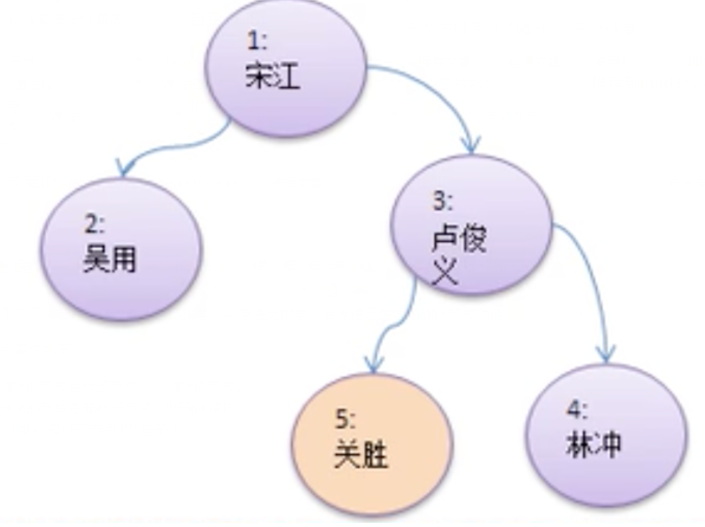
完成一个如下二叉树节点存储、前序遍历搜索、中序遍历搜索、后序遍历搜索和删除节点功能。
对于删除节点要求如下:
代码案例
packagecom.xie.tree;
publicclassBinaryTreeDemo{
publicstaticvoidmain(String[]args){
BinaryTreebinaryTree=newBinaryTree();
HeroNoderoot=newHeroNode(1,"宋江");
HeroNodenode2=newHeroNode(2,"吴用");
HeroNodenode3=newHeroNode(3,"卢俊义");
HeroNodenode4=newHeroNode(4,"林冲");
HeroNodenode5=newHeroNode(5,"关胜");
//先手动创建该二叉树,后面用递归方式
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//前序遍历
System.out.println("前序遍历");
binaryTree.preOrder();
//中序遍历
System.out.println("中序遍历");
binaryTree.infixOrder();
//后续遍历
System.out.println("后续遍历");
binaryTree.postOrder();
//前序遍历查找
System.out.println("前序遍历查找~~");
HeroNoderesultNode=binaryTree.preOrderSearch(5);
if(resultNode!=null){
System.out.printf("找到了,信息为no=%d,name=%s\\n",resultNode.getNo(),resultNode.getName());
System.out.println("遍历次数:"+HeroNode.preCount);
}else{
System.out.println("没有找到");
}
//中序遍历查找
System.out.println("中序遍历查找~~");
HeroNoderesultNode1=binaryTree.infixOrderSearch(5);
if(resultNode1!=null){
System.out.printf("找到了,信息为no=%d,name=%s\\n",resultNode1.getNo(),resultNode1.getName());
System.out.println("遍历次数:"+HeroNode.infoxCount);
}else{
System.out.println("没有找到");
}
//后序遍历查找
System.out.println("后序遍历查找~~");
HeroNoderesultNode2=binaryTree.postOrderSearch(5);
if(resultNode2!=null){
System.out.printf("找到了,信息为no=%d,name=%s\\n",resultNode2.getNo(),resultNode2.getName());
System.out.println("遍历次数:"+HeroNode.postCount);
}else{
System.out.println("没有找到");
}
System.out.println("删除3号节点");
binaryTree.delNo(3);
System.out.println("删除后的节点");
binaryTree.preOrder();
/**
*前序遍历
*HeroNode{no=1,name=宋江}
*HeroNode{no=2,name=吴用}
*HeroNode{no=3,name=卢俊义}
*HeroNode{no=5,name=关胜}
*HeroNode{no=4,name=林冲}
*中序遍历
*HeroNode{no=2,name=吴用}
*HeroNode{no=1,name=宋江}
*HeroNode{no=5,name=关胜}
*HeroNode{no=3,name=卢俊义}
*HeroNode{no=4,name=林冲}
*后续遍历
*HeroNode{no=2,name=吴用}
*HeroNode{no=5,name=关胜}
*HeroNode{no=4,name=林冲}
*HeroNode{no=3,name=卢俊义}
*HeroNode{no=1,name=宋江}
*前序遍历查找~~
*找到了,信息为no=5,name=关胜
*遍历次数:4
*中序遍历查找~~
*找到了,信息为no=5,name=关胜
*遍历次数:3
*后序遍历查找~~
*找到了,信息为no=5,name=关胜
*遍历次数:2
*删除3号节点
*删除后的节点
*HeroNode{no=1,name=宋江}
*HeroNode{no=2,name=吴用}
*/
}
}
classBinaryTree{
privateHeroNoderoot;
publicvoidsetRoot(HeroNoderoot){
this.root=root;
}
//前序遍历
publicvoidpreOrder(){
if(this.root!=null){
this.root.preOrder();
}
}
//中序遍历
publicvoidinfixOrder(){
if(this.root!=null){
this.root.infixOrder();
}
}
//删除节点
publicvoiddelNo(intno){
if(this.root!=null){
if(this.root.getNo()==no){
this.root=null;
}else{
this.root.delNo(no);
}
}
return;
}
//后序遍历
publicvoidpostOrder(){
if(this.root!=null){
this.root.postOrder();
}
}
//前序遍历查找
publicHeroNodepreOrderSearch(intno){
if(root!=null){
returnroot.preOrderSearch(no);
}else{
returnnull;
}
}
//中序遍历查找
publicHeroNodeinfixOrderSearch(intno){
if(root!=null){
returnroot.infixOrderSearch(no);
}else{
returnnull;
}
}
//后序遍历查找
publicHeroNodepostOrderSearch(intno){
if(root!=null){
returnroot.postOrderSearch(no);
}else{
returnnull;
}
}
}
classHeroNode{
staticintpreCount=0;
staticintinfoxCount=0;
staticintpostCount=0;
privateintno;
privateStringname;
privateHeroNodeleft;
privateHeroNoderight;
publicHeroNode(intno,Stringname){
this.no=no;
this.name=name;
}
publicintgetNo(){
returnno;
}
publicvoidsetNo(intno){
this.no=no;
}
publicStringgetName(){
returnname;
}
publicvoidsetName(Stringname){
this.name=name;
}
publicHeroNodegetLeft(){
returnleft;
}
publicvoidsetLeft(HeroNodeleft){
this.left=left;
}
publicHeroNodegetRight(){
returnright;
}
publicvoidsetRight(HeroNoderight){
this.right=right;
}
@Override
publicStringtoString(){
return"HeroNode{"+
"no="+no+
",name="+name+
'}';
}
//前序遍历
publicvoidpreOrder(){
System.out.println(this);
//递归向左子树前序遍历
if(this.left!=null){
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right!=null){
this.right.preOrder();
}
}
//中序遍历
publicvoidinfixOrder(){
//递归向左子树中序遍历
if(this.left!=null){
this.left.infixOrder();
}
System.out.println(this);
//递归向右子树中序遍历
if(this.right!=null){
this.right.infixOrder();
}
}
//后序遍历
publicvoidpostOrder(){
//递归向左子树后序遍历
if(this.left!=null){
this.left.postOrder();
}
//递归向右子树后序遍历
if(this.right!=null){
this.right.postOrder();
}
System.out.println(this);
}
//递归删除节点
//1.如果删除的节点是叶子节点,则删除该节点。
//2.如果删除的节点是非叶子节点,则删除该树。
publicvoiddelNo(intno){
/**
*1.因为我们的二叉树是单向的,所以我们是判断当前节点的子节点是否是需要删除的节点,而不能去判断当前节点是否是需要删除的节点。
*2.如果当前节点的左子节点不为空,并且左子节点就是需要删除的节点,就将this.left=null;并且返回(结束递归)。
*3.如果当前节点的右子节点不为空,并且右子节点就是需要删除的节点,将将this.right=null;并且返回(结束递归)。
*4.如果第2步和第3步没有删除节点,那么就要向左子树进行递归删除。
*5.如果第4步也没有删除节点,则应当向右子树进行递归删除。
*/
if(this.left!=null&&this.left.no==no){
this.left=null;
return;
}
if(this.right!=null&&this.right.no==no){
this.right=null;
return;
}
if(this.left!=null){
this.left.delNo(no);
}
if(this.right!=null){
this.right.delNo(no);
}
}
//前序遍历查找
publicHeroNodepreOrderSearch(intno){
HeroNoderes=null;
preCount++;//这里必须放在this.no==no判断之前,才进行实际的比较
//若果找到,就返回
if(this.no==no){
returnthis;
}
//没有找到,向左子树递归进行前序查找
if(this.left!=null){
res=this.left.preOrderSearch(no);
}
//如果res!=null就直接返回
if(res!=null){
returnres;
}
if(this.right!=null){
res=this.right.preOrderSearch(no);
}
//如果找到就返回
if(res!=null){
returnres;
}
returnres;
}
//中序遍历查找
publicHeroNodeinfixOrderSearch(intno){
HeroNoderes=null;
if(this.left!=null){
res=this.left.infixOrderSearch(no);
}
if(res!=null){
returnres;
}
infoxCount++;//这里必须放在this.no==no判断之前,才进行实际的比较
if(this.no==no){
returnthis;
}
if(this.right!=null){
res=this.right.infixOrderSearch(no);
}
if(res!=null){
returnres;
}
returnres;
}
//后序遍历查找
publicHeroNodepostOrderSearch(intno){
HeroNoderes=null;
if(this.left!=null){
res=this.left.postOrderSearch(no);
}
if(res!=null){
returnres;
}
if(this.right!=null){
res=this.right.postOrderSearch(no);
}
if(res!=null){
returnres;
}
postCount++;//这里必须放在this.no==no判断之前,才进行实际的比较
if(this.no==no){
returnthis;
}
returnres;
}
}
原文地址:https://www.toutiao.com/i6935051711136416287/