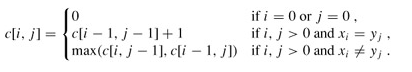本文实例讲述了java基于动态规划法实现求最长公共子序列及最长公共子字符串。分享给大家供大家参考，具体如下：
动态规划法
经常会遇到复杂问题不能简单地分解成几个子问题，而会分解出一系列的子问题。简单地采用把大问题分解成子问题，并综合子问题的解导出大问题的解的方法，问题求解耗时会按问题规模呈幂级数增加。
为了节约重复求相同子问题的时间，引入一个数组，不管它们是否对最终解有用，把所有子问题的解存于该数组中，这就是动态规划法所采用的基本方法。
【问题】 求两字符序列的最长公共字符子序列
问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列x=“x0，x1，…，xm-1”，序列y=“y0，y1，…，yk-1”是x的子序列，存在x的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij=yj。例如，x=“abcbdab”，y=“bcdb”是x的一个子序列。
考虑最长公共子序列问题如何分解成子问题，设a=“a0，a1，…，am-1”，b=“b0，b1，…，bm-1”，并z=“z0，z1，…，zk-1”为它们的最长公共子序列。不难证明有以下性质：
（1） 如果am-1=bn-1，则zk-1=am-1=bn-1，且“z0，z1，…，zk-2”是“a0，a1，…，am-2”和“b0，b1，…，bn-2”的一个最长公共子序列；
（2） 如果am-1!=bn-1，则若zk-1!=am-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列；
（3） 如果am-1!=bn-1，则若zk-1!=bn-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列。
这样，在找a和b的公共子序列时，如有am-1=bn-1，则进一步解决一个子问题，找“a0，a1，…，am-2”和“b0，b1，…，bm-2”的一个最长公共子序列；如果am-1!=bn-1，则要解决两个子问题，找出“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列和找出“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列，再取两者中较长者作为a和b的最长公共子序列。
求解：
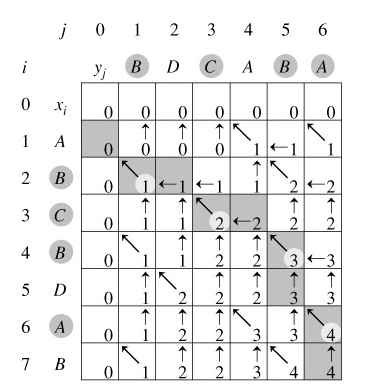
引进一个二维数组c[][]，用c[i][j]记录x[i]与y[j] 的lcs 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。
我们是自底向上进行递推计算，那么在计算c[i,j]之前，c[i-1][j-1]，c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据x[i] = y[j]还是x[i] != y[j]，就可以计算出c[i][j]。
问题的递归式写成：
回溯输出最长公共子序列过程：
算法分析：
由于每次调用至少向上或向左（或向上向左同时）移动一步，故最多调用(m * n)次就会遇到i = 0或j = 0的情况，此时开始返回。返回时与递归调用时方向相反，步数相同，故算法时间复杂度为θ(m * n)。
java代码实现：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
public class lcsproblem
{
public static void main(string[] args)
{
//保留空字符串是为了getlength()方法的完整性也可以不保留
//但是在getlength()方法里面必须额外的初始化c[][]第一个行第一列
string[] x = {"", "a", "b", "c", "b", "d", "a", "b"};
string[] y = {"", "b", "d", "c", "a", "b", "a"};
int[][] b = getlength(x, y);
display(b, x, x.length-1, y.length-1);
}
/**
* @param x
* @param y
* @return 返回一个记录决定搜索的方向的数组
*/
public static int[][] getlength(string[] x, string[] y)
{
int[][] b = new int[x.length][y.length];
int[][] c = new int[x.length][y.length];
for(int i=1; i<x.length; i++)
{
for(int j=1; j<y.length; j++)
{
//对应第一个性质
if( x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 1;
}
//对应第二或者第三个性质
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 0;
}
//对应第二或者第三个性质
else
{
c[i][j] = c[i][j-1];
b[i][j] = -1;
}
}
}
return b;
}
//回溯的基本实现，采取递归的方式
public static void display(int[][] b, string[] x, int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == 1)
{
display(b, x, i-1, j-1);
system.out.print(x[i] + " ");
}
else if(b[i][j] == 0)
{
display(b, x, i-1, j);
}
else if(b[i][j] == -1)
{
display(b, x, i, j-1);
}
}
}
|
运行结果：
b c b a
最长公共子字符串：类似最长子序列，只是公共子字符串要求必须是连续的。
java实现代码如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
public class stringcompare {
//在动态规划矩阵生成方式当中，每生成一行，前面的那一行就已经没有用了，因此这里只需使用一维数组，而不是常用的二位数组
public static void getlcstring(char[] str1, char[] str2) {
int len1, len2;
len1 = str1.length;
len2 = str2.length;
int maxlen = len1 > len2 ? len1 : len2;
int[] max = new int[maxlen];// 保存最长子串长度的数组
int[] maxindex = new int[maxlen];// 保存最长子串长度最大索引的数组
int[] c = new int[maxlen];
int i, j;
for (i = 0; i < len2; i++) {
for (j = len1 - 1; j >= 0; j--) {
if (str2[i] == str1[j]) {
if ((i == 0) || (j == 0))
c[j] = 1;
else
c[j] = c[j - 1] + 1;//此时c[j-1]还是上次循环中的值，因为还没被重新赋值
} else {
c[j] = 0;
}
// 如果是大于那暂时只有一个是最长的,而且要把后面的清0;
if (c[j] > max[0]) {
max[0] = c[j];
maxindex[0] = j;
for (int k = 1; k < maxlen; k++) {
max[k] = 0;
maxindex[k] = 0;
}
}
// 有多个是相同长度的子串
else if (c[j] == max[0]) {
for (int k = 1; k < maxlen; k++) {
if (max[k] == 0) {
max[k] = c[j];
maxindex[k] = j;
break; // 在后面加一个就要退出循环了
}
}
}
}
for (int temp : c) {
system.out.print(temp);
}
system.out.println();
}
//打印最长子字符串
for (j = 0; j < maxlen; j++) {
if (max[j] > 0) {
system.out.println("第" + (j + 1) + "个公共子串:");
for (i = maxindex[j] - max[j] + 1; i <= maxindex[j]; i++)
system.out.print(str1[i]);
system.out.println(" ");
}
}
}
public static void main(string[] args) {
string str1 = new string("binghaven");
string str2 = new string("jingseven");
getlcstring(str1.tochararray(), str2.tochararray());
}
}
|
输出：
000000000
010000000
002000001
000300000
000000000
000000010
000000100
000000020
001000003
第1个公共子串:
ing
第2个公共子串:
ven
希望本文所述对大家java程序设计有所帮助。
原文链接：https://blog.csdn.net/u013063153/article/details/49593353
相关文章
- 64M VPS建站：是否适合初学者操作和管理？ 2025-06-10
- ASP.NET自助建站系统中的用户注册和登录功能定制方法 2025-06-10
- ASP.NET自助建站系统的域名绑定与解析教程 2025-06-10
- 个人服务器网站搭建：如何选择合适的服务器提供商？ 2025-06-10
- ASP.NET自助建站系统中如何实现多语言支持？ 2025-06-10
