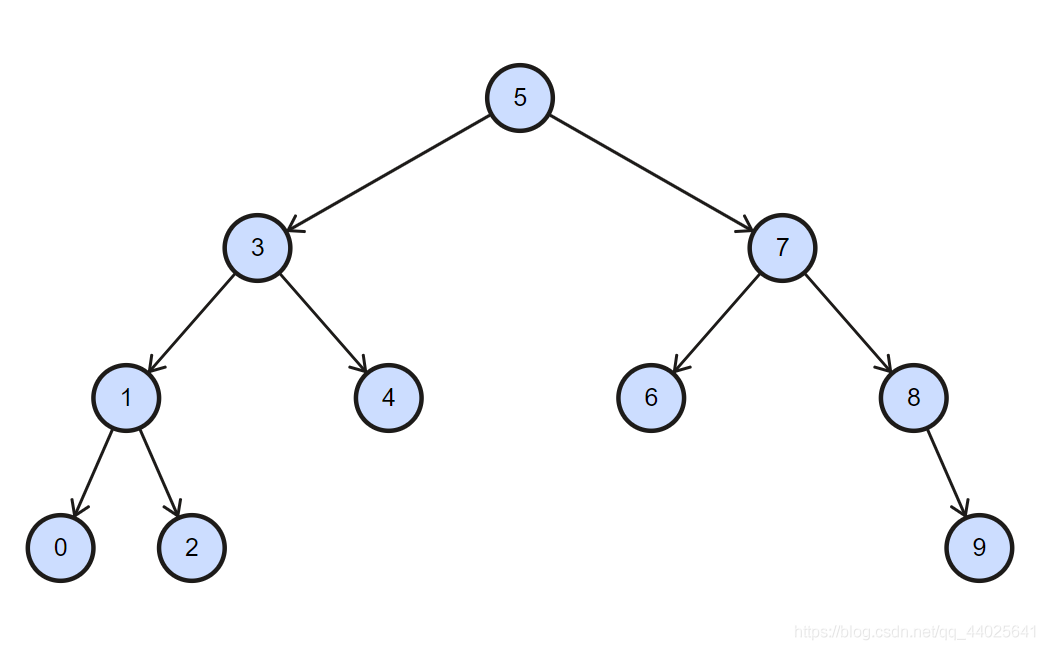
二叉搜索树的定义
- 它是一颗二叉树
- 任一节点的左子树上的所有节点的值一定小于该节点的值
- 任一节点的右子树上的所有节点的值一定大于该节点的值
特点： 二叉搜索树的中序遍历结果是有序的（升序）！
实现一颗二叉搜索树
二叉搜索树的定义类
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public class bst {
static class node {
private int key;
private node left;
private node right;
public node(int key) {
this.key = key;
}
}
private node root;//bst的根节点
}
|
二叉搜索树的查找
- 二叉搜索树的查找思路：
- ①如果要查找的值等于当前节点的值，那么，就找到了
- ②如果要查找的值小于当前节点的值，那么，就往当前节点的左子树走
- ③如果要查找的值大于当前节点的值，那么，就往当前节点的右子树走
-
最终，如果走到空了还没有找到，就说明不存在这个
key
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
/**
* 查找是否存在节点
*
* 思路：根据二叉排序树的特点：
* ①如果要查找的值小于当前节点的值，那么，就往当前节点的左子树走
* ②如果要查找的值大于当前节点的值，那么，就往当前节点的右子树走
*
* @param key 带查找的key
* @return boolean是否存在
*/
public boolean find(int key) {
node cur = root;
while (cur != null) {
if (key < root.key) {
cur = cur.left;
} else if (key > root.key) {
cur = cur.right;
} else {
return true;
}
}
return false;
}
|
二叉搜索树的插入
- 二叉搜索树的插入思路：
-
思路和查找一样的，只是我们这次要进行的是插入操作，那么我们还需要一个
parent节点，来时刻记录当前节点的双亲节点即： -
①如果要插入的值等于当前节点的值，那么，无法插入（不可出现重复的
key） - ②如果要插入的值小于当前节点的值，那么，就往当前节点的左子树走
- ③如果要插入的值大于当前节点的值，那么，就往当前节点的右子树走
-
最终，如果走到空了，就说明不存在重复的
key，只要往双亲节点的后面插就好了，就是合适的位置，具体往左边还是右边插入，需要比较待插入节点的key和parent的key
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
/**
* 往二叉树中插入节点
*
* 思路如下：
*
* @param key 待插入的节点
*/
public void insert(int key) {
if (root == null) { //如果是空树，那么，直接插入
root = new node(key);
return;
}
node cur = root;
node parent = null; //parent 为cur的父节点
while (true) {
if (cur == null) { //在遍历过程中，找到了合适是位置，就指针插入（没有重复节点）
if (parent.key < key) {
parent.right = new node(key);
} else {
parent.left = new node(key);
}
return;
}
if (key < cur.key) {
parent = cur;
cur = cur.left;
} else if (key > cur.key) {
parent = cur;
cur = cur.right;
} else {
throw new runtimeexception("插入失败，已经存在key");
}
}
}
|
二叉搜索树的删除
- 二叉搜索树的删除思路：（详细的思路看注释）
-
首先，需要先找到是否存在
key节点，如果存在，则删除，如果不存在则删除错误 - 对于，如果存在，则分为三种情况：
- ①要删除的节点，没有左孩子
ⅰ：要删除的节点为根节点：root = delete.right;
ⅱ：要删除的节点为其双亲节点的左孩子：parent.left = delete.right;
ⅲ：要删除的节点为其双亲节点的右孩子：parent.right = delete.right;
- ②要删除的节点，没有右孩子
ⅰ：要删除的节点为根节点：root = delete.left;
ⅱ：要删除的节点为其双亲节点的左孩子：parent.left = delete.left;
ⅲ：要删除的节点为其双亲节点的右孩子：parent.right = delete.left;
- ③要删除的节点，既有左孩子又有右孩子：
此时我们需要找到整颗二叉树中第一个大于待删除节点的节点，然后替换他俩的值，最后，把找到的节点删除
ⅰ：找到的节点的双亲节点为待删除的节点：delete.key = find.key; findparent.right = find.right;
ⅱ：找到的节点的双亲节点不是待删除的节点：delete.key = find.key; findparent.left = find.right;
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
|
/**
* 删除树中节点
*
* 思路如下：
*
* @param key 待删除的节点
*/
public void remove(int key) {
if (root == null) {
throw new runtimeexception("为空树，删除错误！");
}
node cur = root;
node parent = null;
//查找是否key节点的位置
while (cur != null) {
if (key < cur.key) {
parent = cur;
cur = cur.left;
} else if (key > cur.key) {
parent = cur;
cur = cur.right;
} else {
break;
}
}
if (cur == null) {
throw new runtimeexception("找不到key，输入key不合法");
}
//cur 为待删除的节点
//parent 为待删除的节点的父节点
/*
* 情况1：如果待删除的节点没有左孩子
* 其中
* ①待删除的节点有右孩子
* ②待删除的节点没有右孩子
* 两种情况可以合并
*/
if (cur.left == null) {
if (cur == root) { //①如果要删除的是根节点
root = cur.right;
} else if (cur == parent.left) { //②如果要删除的是其父节点的左孩子
parent.left = cur.right;
} else { //③如果要删除的节点为其父节点的右孩子
parent.right = cur.right;
}
}
/*
* 情况2:如果待删除的节点没有右孩子
*
* 其中:待删除的节点必定存在左孩子
*/
else if (cur.right == null) { //①如果要删除的是根节点
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) { //②如果要删除的是其父节点的左孩子
parent.left = cur.left;
} else { //③如果要删除的节点为其父节点的右孩子
parent.right = cur.left;
}
}
/*
* 情况3:如果待删除的节点既有左孩子又有右孩子
*
* 思路:
* 因为是排序二叉树,要找到整颗二叉树第一个大于该节点的节点,只需要,先向右走一步,然后一路往最左走就可以找到了
* 因此:
* ①先向右走一步
* ②不断向左走
* ③找到第一个大于待删除的节点的节点,将该节点的值,替换到待删除的节点
* ④删除找到的这个节点
* ⑤完成删除
*
*/
else {
node nextparent = cur; //定义父节点,初始化就是待删除的节点
node next = cur.right; //定义next为当前走到的节点,最终目的是找到第一个大于待删除的节点
while (next.left != null) {
nextparent = next;
next = next.left;
}
cur.key = next.key; //找到之后,完成值的替换
if (nextparent == cur) { //此时的父节点就是待删除的节点,那么说明找到的节点为父节点的右孩子(因为此时next只走了一步)
nextparent.right = next.right;
} else { //此时父节点不是待删除的节点,即next确实往左走了,且走到了头.
nextparent.left = next.right;
}
}
}
|
到此这篇关于利用java实现二叉搜索树的文章就介绍到这了,更多相关java二叉搜索树内容请搜索快网idc以前的文章或继续浏览下面的相关文章希望大家以后多多支持快网idc！
原文链接：https://blog.csdn.net/qq_44025641/article/details/115712153
相关文章
猜你喜欢
- ASP.NET自助建站系统中如何实现多语言支持？ 2025-06-10
- 64M VPS建站：如何选择最适合的网站建设平台？ 2025-06-10
- ASP.NET本地开发时常见的配置错误及解决方法？ 2025-06-10
- ASP.NET自助建站系统的数据库备份与恢复操作指南 2025-06-10
- 个人网站服务器域名解析设置指南：从购买到绑定全流程 2025-06-10
