比如向量(31,-41,59,26,-53,58,97,-93,-23,84);
最大和是从59到97即为187
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
|
#include<stdio.h>
#include<stdlib.h>
//两者的最大值
int max( int x, int y );
//三者的最大值
int max2( int x, int y, int z );
//最原始的算法，复杂度为T(n)=O(n*n)
int oringinal( int v[], int len );
//原始基础上变体版,复杂度为T(n)=O(n*n)
int oringinal_ex( int v[], int len );
//分治法,复杂度为T(n)=O(n*log(n))
/*
*分治法的思想是：将原数组分成两部分，要求的最大值
*要么在左边这部分里面，要么在右边这部分里面
*要么就在左右相交的交界处
*/
int divAndCon( int v[], int low, int high );
//扫描法,复杂度为T(n)=O(n)
int scan(int v[], int len);
void main()
{
int i = 0;
int v[] = {31,-41,59,26,-53,58,97,-93,-23,84};
int len = 0;
int result;
len = sizeof(v) / sizeof(int);
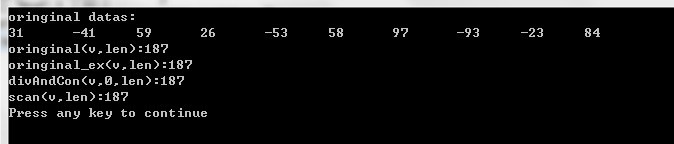
printf("oringinal datas:\\n");
for( i = 0; i < len; i++ )
{
printf("%d\\t",v[i]);
}
printf("\\n");
//最原始的算法
result = oringinal(v,len);
printf("oringinal(v,len):%d\\n",result);
//最原始变体的算法
result = oringinal_ex(v,len);
printf("oringinal_ex(v,len):%d\\n",result);
//分治法
result = divAndCon(v,0,len-1);
printf("divAndCon(v,0,len):%d\\n",result);
//扫描法
result = scan(v,len);
printf("scan(v,len):%d\\n",result);
}
//两者的最大值
int max( int x, int y )
{
if( x < y )
{
x = y;
}
return x;
}
//三者的最大值
int max2( int x, int y, int z )
{
if( x < y )
{
x = y;
}
if( x < z )
{
x = z;
}
return x;
}
//最原始的算法，复杂度为T(n)=O(n*n)
int oringinal( int v[], int len )
{
int maxsofar = 0;
int i;
int j;
int sum = 0;
//通过双层循环逐步扫描，通过max( sum, maxsofar)获得当前最大值
for( i = 0; i < len; i++ )
{
sum = 0;
for( j = i; j < len; j++ )
{
sum += v[j];
maxsofar = max( sum, maxsofar );
}
}
return maxsofar;
}
//原始基础上变体版,复杂度为T(n)=O(n*n)
int oringinal_ex( int v[], int len )
{
int i = 0;
int j = 0;
int sum = 0;
int maxsofar = 0;
int *cumarr = ( int * )malloc( len * sizeof(int) );
for( i = 0; i < len; i++ )
{
if( i == 0 )
{
cumarr[0] = v[i];
}
else
{
cumarr[i] = cumarr[i-1] + v[i];
}
}
for( i = 0; i < len; i++ )
for( j = i; j < len; j++ )
{
if( i == 0 )
{
sum = cumarr[i];
}
else
{
sum = cumarr[j] - cumarr[i-1];
}
maxsofar = max(maxsofar,sum);
}
return maxsofar;
}
//分治法,复杂度为T(n)=O(n*log(n))
int divAndCon( int v[], int low, int high )
{
int mid = 0;
int lmax = 0;
int rmax = 0;
int sum = 0;
int i = 0;
if( low > high )
{
return 0;
}
if( low == high )
{
return max(0,v[low]);
}
mid = ( low + high ) / 2;
lmax = sum = 0;
for( i = mid; i >= low; i-- )
{
sum += v[i];
lmax = max(lmax,sum);
}
rmax = sum = 0;
for( i = mid + 1; i <= high; i++ )
{
sum +=v[i];
rmax = max(rmax,sum);
}
return max2(lmax + rmax,divAndCon(v,low,mid),divAndCon(v,mid+1,high));
}
//扫描法,复杂度为T(n)=O(n)
int scan(int v[], int len)
{
int maxsofar = 0;
int maxendinghere = 0;
int i = 0;
for( i =0; i < len; i++ )
{
maxendinghere = max(maxendinghere + v[i],0);
maxsofar = max(maxsofar,maxendinghere);
}
return maxsofar;
}
|
比如向量(31,-41,59,26,-53,58,97,-93,-23,84);
最大和是从97到-93即为4
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#include<stdio.h>
#include<math.h>
//返回最接近0的数
int closeZero( int x, int y );
//最原始的算法，复杂度为T(n)=O(n*n)
int oringinal( int v[], int len );
void main()
{
int i = 0;
int v[] = {31,-41,59,26,-53,58,97,-93,-23,84};
int len = 0;
int result;
len = sizeof(v) / sizeof(int);
printf("oringinal datas:\\n");
for( i = 0; i < len; i++ )
{
printf("%d\\t",v[i]);
}
printf("\\n");
//最原始的算法
result = oringinal(v,len);
printf("oringinal(v,len):%d\\n",result);
}
//返回最接近0的数
int closeZero( int x, int y )
{
if( abs(x) > abs(y) )
{
x = y;
}
return x;
}
//最原始的算法，复杂度为T(n)=O(n*n)
int oringinal( int v[], int len )
{
int sofar = v[0];
int i;
int j;
int sum = 0;
for( i = 0; i < len; i++ )
{
sum = 0;
for( j = i; j < len; j++ )
{
sum += v[j];
sofar = closeZero( sum, sofar );
}
}
return sofar;
}
|
运行结果：
相关文章
猜你喜欢
- ASP.NET自助建站系统中的用户注册和登录功能定制方法 2025-06-10
- ASP.NET自助建站系统的域名绑定与解析教程 2025-06-10
- 个人服务器网站搭建：如何选择合适的服务器提供商？ 2025-06-10
- ASP.NET自助建站系统中如何实现多语言支持？ 2025-06-10
- 64M VPS建站：如何选择最适合的网站建设平台？ 2025-06-10
