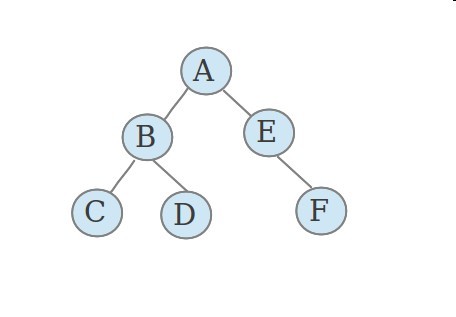
二叉树的遍历本质上其实就是入栈出栈的问题，递归算法简单且容易理解，但是效率始终是个问题。非递归算法可以清楚的知道每步实现的细节，但是乍一看不想递归算法那么好理解，各有各的好处吧。接下来根据下图讲讲树的遍历。
1、先序遍历：先序遍历是先输出根节点，再输出左子树，最后输出右子树。上图的先序遍历结果就是：ABCDEF
2、中序遍历：中序遍历是先输出左子树，再输出根节点，最后输出右子树。上图的中序遍历结果就是：CBDAEF
3、后序遍历：后序遍历是先输出左子树，再输出右子树，最后输出根节点。上图的后序遍历结果就是：CDBFEA
其中，后序遍历的非递归算法是最复杂的，我用了一个标识符isOut来表明是否需要弹出打印。因为只有当节点的左右子树都打印后该节点 才能弹出栈打印，所以标识isOut为1时打印，isOut初始值为0，这主要是为了处理非叶子节点。由后序遍历的原理决定，左右子树都被打印该节点才能打印，所以该节点肯定会被访问2次，第一次的时候不要打印，第二次打印完右子树的时候打印。叶子节点打印完后将isOut置为1。（纯粹是自己想的，应该还有逻辑更简单的算法）
实例
构造和遍历
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE//节点结构
{
struct _NODE* leftChild;
int value;
struct _NODE* rightChild;
} NODE, *PNODE;
PNODE createNode(int value){//创建一个新节点
PNODE n = (PNODE)malloc(sizeof(NODE));
n->value = value;
n->leftChild = NULL;
n->rightChild = NULL;
return n;
}
PNODE insertLeftChild(PNODE parent, int value){//在指定节点上插入左节点
return (parent->leftChild = createNode(value));
}
PNODE insertRightChild(PNODE parent, int value){//在指定节点上插入左节点
return (parent->rightChild = createNode(value));
}
void createBTree(PNODE root, int i){//向树中插入一些元素
if (i == 0)
{
return;
}
else{
PNODE l = insertLeftChild(root, i * 10 + 1);
PNODE r = insertRightChild(root, i * 10 + 2);
createBTree(l, --i);
createBTree(r, i);
}
}
void printDLR(PNODE root){//先序遍历：对每一刻子树都是根->左->右的顺序
if (root == NULL)
{
return;
}
printf("%-4d", root->value);
printDLR(root->leftChild);
printDLR(root->rightChild);
}
void printLDR(PNODE root){//中序遍历：
if (root == NULL)
{
return;
}
printLDR(root->leftChild);
printf("%-4d", root->value);
printLDR(root->rightChild);
}
void printLRD(PNODE root){//后序遍历
if (root == NULL)
{
return;
}
printLRD(root->leftChild);
printLRD(root->rightChild);
printf("%-4d", root->value);
}
void main(){
PNODE root = createNode(0);//创建根节点
createBTree(root, 3);
printf("先序遍历: ");
printDLR(root);//遍历
printf("\\n中序遍历: ");
printLDR(root);
printf("\\n后序遍历: ");
printLRD(root);
printf("\\n");
}
|
执行结果：
先序遍历：
中序遍历：
后序遍历：
C++中可以使用类模板，从而使节点值的类型可以不止限定在整型：
?
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
|
#include <iostream.h>
template <class T> class Node//节点类模板
{
public:
Node(T value):value(value)//构造方法
{
leftChild = 0;
rightChild = 0;
}
Node* insertLeftChild(T value);//插入左孩子,返回新节点指针
Node* insertRightChild(T vallue);//插入右孩子
void deleteLeftChild();//删左孩子
void deleteRightChild();//删右孩子
void showDLR();//先序遍历
void showLDR();//中序遍历
void showLRD();//后序遍历
protected:
T value;//节点值
Node* leftChild;//左孩子指针
Node* rightChild;//右孩子指针
private:
};
template <class T> Node<T>* Node<T>::insertLeftChild(T value){//插入左孩子
return (this->leftChild = new Node(value));
}
template <class T> Node<T>* Node<T>::insertRightChild(T value){//插入右孩子
return (this->rightChild = new Node(value));
}
template <class T> void Node<T>::deleteLeftChild(){//删除左孩子
delete this->leftChild;
this->leftChild = 0;
}
template <class T> void Node<T>::deleteRightChild(){//删除右孩子
delete this->rightChild;
this->rightChild = 0;
}
template <class T> void Node<T>::showDLR(){//先序遍历
cout<<this->value<<" ";
if (leftChild)
{
leftChild->showDLR();
}
if (rightChild)
{
rightChild->showDLR();
}
}
template <class T> void Node<T>::showLDR(){//中序遍历
if (leftChild)
{
leftChild->showLDR();
}
cout<<this->value<<" ";
if (rightChild)
{
rightChild->showLDR();
}
}
template <class T> void Node<T>::showLRD(){//后序遍历
if (leftChild)
{
leftChild->showLRD();
}
if (rightChild)
{
rightChild->showLRD();
}
cout<<this->value<<" ";
}
template <class T> void createSomeNodes(Node<T>* root, int i, T base){//构建一个二叉树
if (i == 0)
{
return;
}
Node<T>* l = root->insertLeftChild(i + base);
Node<T>* r = root->insertRightChild(i + base);
createSomeNodes(l, --i, base);
createSomeNodes(r, i, base);
}
template <class T> void showTest(Node<T>* root){//显示各种遍历方式结果
cout<<"先序遍历: ";
root->showDLR();
cout<<endl<<"中序遍历: ";
root->showLDR();
cout<<endl<<"后序遍历: ";
root->showLRD();
cout<<endl;
}
void main(){
Node<int> *root1 = new Node<int>(0);
createSomeNodes(root1, 3, 0);
cout<<"整型:"<<endl;
showTest(root1);
Node<char> *root2 = new Node<char>('a');
createSomeNodes(root2, 3, 'a');
cout<<"字符型:"<<endl;
showTest(root2);
Node<float> *root3 = new Node<float>(0.1f);
createSomeNodes(root3, 3, 0.1f);
cout<<"浮点型:"<<endl;
showTest(root3);
}
|
相关文章
猜你喜欢
- 个人服务器网站搭建：如何选择适合自己的建站程序或框架？ 2025-06-10
- 64M VPS建站：能否支持高流量网站运行？ 2025-06-10
- 64M VPS建站：怎样选择合适的域名和SSL证书？ 2025-06-10
- 64M VPS建站：怎样优化以提高网站加载速度？ 2025-06-10
- 64M VPS建站：是否适合初学者操作和管理？ 2025-06-10
