树,二叉树(完全二叉树,满二叉树)概念图解

也想出现在这里？点击联系我~

1、树的定义

树是n个结点的有限集合，有且仅有一个根结点，其余结点可分为m个根结点的子树。

2、树的概念

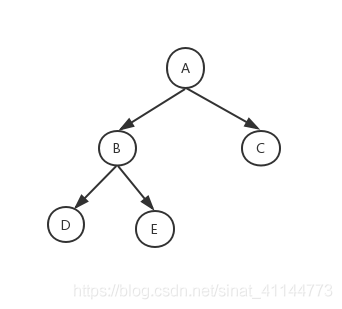
1. 结点的度:一个结点拥有子树的个数称为度。比如A的度为3，C的度为2，H的度为0。度为0的结点称为叶子节点（D,F,G,H）。树的度是树中所有结点的度的最大值，此树的度为3。
2. 树中结点的最大层次成为树的深度或高度。此树的深度为4。
3. 父节点A的子结点B,C,D；B,C,D也是兄弟节点
4. 树的集合称为森林.树和森林之间有着密切的关系.删除一个树的根结点,其所有原来的子树都是树,构成森林.用一个结点连接到森林的所有树的根结点就构成树.

3、二叉树

二叉树是每个节点最多拥有两个子节点，左子树和右子树是有顺序的不能任意颠倒。

4、二叉树遍历

前序遍历（前根遍历）：根——>左——>右

中序遍历（中根遍历）：左——>根——>右

后序遍历（后根遍历）：左——>右——>根

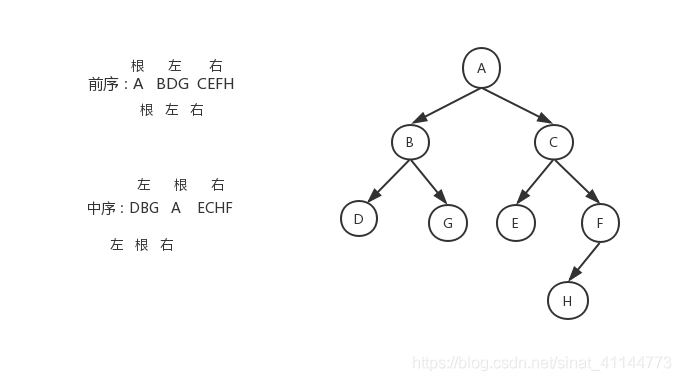
已知前序和中序，求后序问题， 前序 ABDGCEFH 中序 DGBAECHF

解法：根据前序、中序综合判断画出树的节点图，然后再写后序遍历：DGBEHFCA

（前序和中序的子树也满足前序或中序的规则）

二叉树的深度优先遍历（DFS）与广度优先遍历（BFS）

DFS深度优先遍历：从根节点出发，沿着左子树方向进行纵向遍历，直到找到叶子节点为止。然后回溯到前一个节点，进行右子树节点的遍历，直到遍历完所有可达节点为止。利用数据结构“栈”，父节点入栈，父节点出栈，先右子节点入栈，后左子节点入栈。递归遍历全部节点。

DFS:ABDGCEFH

BFS广度优先遍历：从根节点出发，在横向遍历二叉树层段节点的基础上纵向遍历二叉树的层次。利用数据结构“队列”，父节点入队，父节点出队列，先左子节点入队，后右子节点入队。递归遍历全部节点。

BFS：ABCDGEFH

5、满二叉树

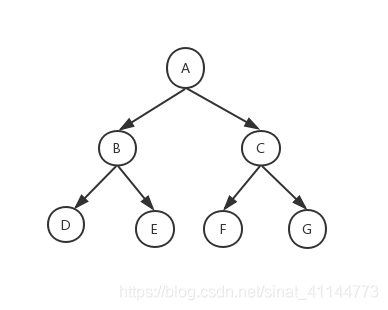
高度为h，由2^h-1个节点构成的二叉树称为满二叉树。

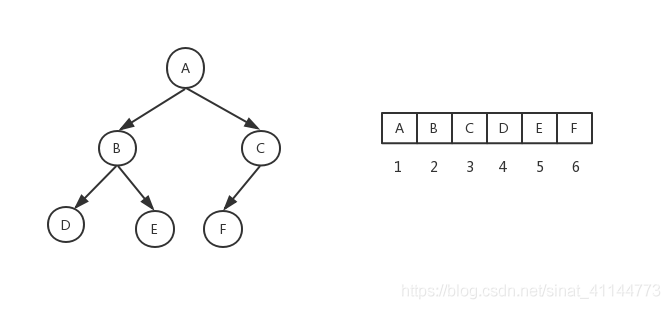
6、完全二叉树

完全二叉树是由满二叉树而引出来的，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

堆一般都是用完全二叉树来实现的。

总结

本篇文章就到这里了，希望可以给你带来一些帮助，也希望您能够多多关注我们的更多内容！

原文链接：https://blog.csdn.net/sinat_41144773/article/details/89530403